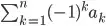5

I am reading a review to compare Mathematica to APL/J. One question raised in the article seems very interesting to me:

Is Mathematica really the way to go to express our creative thoughts – viz back to a 17th century notation designed for parchment instead of forward to a twentieth-century one designed for computers?

Can one share examples of Iverson's notation vs traditional math notation to demonstrate the edge of APL/J on expressing and solving math problems? This would be greatly helpful for new comers.

ahala
  • 4,683
  • 5
  • 27
  • 36
  • 5
    This question appears to be off-topic because it is about alternate mathematical notations rather than a specific programming problem. – Jim Lewis Jan 22 '14 at 19:28
  • 1
    Keep in mind that the document you linked is rather biased, since the author calls himself an "active APLer". – Stefano Sanfilippo Jan 22 '14 at 19:39

2 Answers2

5

One example: Alternating series.

Alternating sum is very common in mathematics. But it is cumbersome to put the sign before each term:

\sum_{k=1}^n (-1)^k a_k

in APL and J, because of the order of operations, it is 

-/a
Tobia
  • 17,856
  • 6
  • 74
  • 93
ahala
  • 4,683
  • 5
  • 27
  • 36
5

I recommend reading Iverson's paper Notation as a Tool of Thought, kindly provided by the J folks. It deals precisely with this issue.

In it you'll find many Math proofs derived using APL instead of the classical notation, along with accompanying commentary. Here's a redacted example, proving Gauss's formula for the arithmetic series:

+/⍳n    
+/⌽⍳n               ⍝ as + is associative and commutative
((+/⍳n)+(+/⌽⍳n))÷2  ⍝ as x=(x+x)÷2
(+/(⍳n)+(⌽⍳n))÷2    ⍝ as + is associative and commutative
(+/(n/n+1))÷2       ⍝ summing each respective x∊⍳n and y∊⌽⍳n, y=n+1-x → (x+y)=n+1
(n×n+1)÷2           ⍝ per definition of × (times)

Other articles by Iverson, Hui and friends are also illuminating. Again, the J folks provide a notable library.

Tobia
  • 17,856
  • 6
  • 74
  • 93