0

we are working on a project and trying to get some results with KPCA.

We have a dataset (handwritten digits) and have taken the 200 first digits of each number so our complete traindata matrix is 2000x784 (784 are the dimensions). When we do KPCA we get a matrix with the new low-dimensionality dataset e.g.2000x100. However we don't understand the result. Shouldn;t we get other matrices such as we do when we do svd for pca? the code we use for KPCA is the following:

function data_out = kernelpca(data_in,num_dim)

%% Checking to ensure output dimensions are lesser than input dimension.
if num_dim > size(data_in,1)
    fprintf('\nDimensions of output data has to be lesser than the dimensions of input data\n');
    fprintf('Closing program\n');
    return 
end

%% Using the Gaussian Kernel to construct the Kernel K
% K(x,y) = -exp((x-y)^2/(sigma)^2)
% K is a symmetric Kernel
K = zeros(size(data_in,2),size(data_in,2));
for row = 1:size(data_in,2)
    for col = 1:row
        temp = sum(((data_in(:,row) - data_in(:,col)).^2));
        K(row,col) = exp(-temp); % sigma = 1
    end
end
K = K + K'; 
% Dividing the diagonal element by 2 since it has been added to itself
for row = 1:size(data_in,2)
    K(row,row) = K(row,row)/2;
end
% We know that for PCA the data has to be centered. Even if the input data
% set 'X' lets say in centered, there is no gurantee the data when mapped
% in the feature space [phi(x)] is also centered. Since we actually never
% work in the feature space we cannot center the data. To include this
% correction a pseudo centering is done using the Kernel.
one_mat = ones(size(K));
K_center = K - one_mat*K - K*one_mat + one_mat*K*one_mat;
clear K

%% Obtaining the low dimensional projection
% The following equation needs to be satisfied for K
% N*lamda*K*alpha = K*alpha
% Thus lamda's has to be normalized by the number of points
opts.issym=1;                          
opts.disp = 0; 
opts.isreal = 1;
neigs = 30;
[eigvec eigval] = eigs(K_center,[],neigs,'lm',opts);
eig_val = eigval ~= 0;
eig_val = eig_val./size(data_in,2);
% Again 1 = lamda*(alpha.alpha)
% Here '.' indicated dot product
for col = 1:size(eigvec,2)
    eigvec(:,col) = eigvec(:,col)./(sqrt(eig_val(col,col)));
end
[~, index] = sort(eig_val,'descend');
eigvec = eigvec(:,index);

%% Projecting the data in lower dimensions
data_out = zeros(num_dim,size(data_in,2));
for count = 1:num_dim
    data_out(count,:) = eigvec(:,count)'*K_center';
end

we have read lots of papers but still cannot get the hand of kpca's logic!

Any help would be appreciated!

Ray
  • 2,472
  • 18
  • 22
user1108001
  • 33
  • 6

1 Answers1

3

PCA Algorithm:

  1. PCA data samples

  2. Compute mean

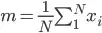
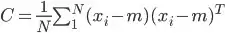
  3. Compute covariance

  4. Solve

: Covariance matrix. 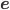: Eigen Vectors of covariance matrix. : Eigen values of covariance matrix.

With the first n-th eigen vectors you reduce the dimensionality of your data to the n dimensions. You can use this code for the PCA, it has an integraded example and it is simple.

KPCA Algorithm:

We choose a kernel function in you code this is specified by:

K(x,y) = -exp((x-y)^2/(sigma)^2)

in order to represent your data in a high dimensional space hopping that, in this space your data will be well represented for further porposes like classification or clustering whereas this task could be harder to be solved in the initial feature space. This trick is aslo known as "Kernel trick". Look figure.

enter image description here

[Step1] Constuct gram matrix

K = zeros(size(data_in,2),size(data_in,2));
for row = 1:size(data_in,2)
    for col = 1:row
        temp = sum(((data_in(:,row) - data_in(:,col)).^2));
        K(row,col) = exp(-temp); % sigma = 1
    end
end
K = K + K'; 
% Dividing the diagonal element by 2 since it has been added to itself
for row = 1:size(data_in,2)
    K(row,row) = K(row,row)/2;
end

Here because the gram matrix is symetric the half of the values are computed and the final result is obtained by adding the computed so far gram matrix and its transpose. Finally, we divide by 2 as the comments mention.

[Step2] Normalize the kernel matrix

This is done by this part of your code: 

K_center = K - one_mat*K - K*one_mat + one_mat*K*one_mat;

As the comments mention a pseudocentering procedure must be done. For an idea about the proof here.

[Step3] Solve the eigenvalue problem

For this task this part of the code is responsible.

%% Obtaining the low dimensional projection
% The following equation needs to be satisfied for K
% N*lamda*K*alpha = K*alpha
% Thus lamda's has to be normalized by the number of points
opts.issym=1;                          
opts.disp = 0; 
opts.isreal = 1;
neigs = 30;
[eigvec eigval] = eigs(K_center,[],neigs,'lm',opts);
eig_val = eigval ~= 0;
eig_val = eig_val./size(data_in,2);
% Again 1 = lamda*(alpha.alpha)
% Here '.' indicated dot product
for col = 1:size(eigvec,2)
    eigvec(:,col) = eigvec(:,col)./(sqrt(eig_val(col,col)));
end
[~, index] = sort(eig_val,'descend');
eigvec = eigvec(:,index);

[Step4] Change representaion of each data point

For this task this part of the code is responsible.

%% Projecting the data in lower dimensions
data_out = zeros(num_dim,size(data_in,2));
for count = 1:num_dim
    data_out(count,:) = eigvec(:,count)'*K_center';
end

Look the details here.

PS: I encurage you to use code written from this author and contains intuitive examples.

Darkmoor
  • 862
  • 11
  • 29