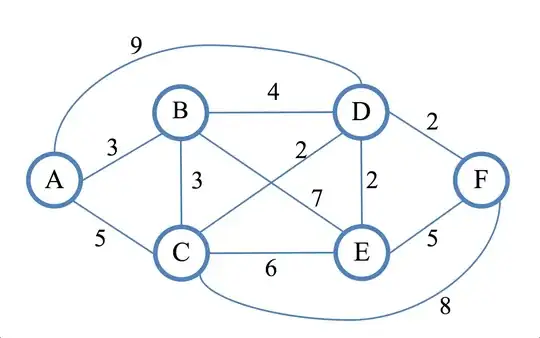
In this network Dijkstra’s shortest-path algorithm is used. The question is which path will A use to reach D because both are equal?
is that table missing?

In this network Dijkstra’s shortest-path algorithm is used. The question is which path will A use to reach D because both are equal?

is that table missing?
It depends on your actual implementation and the way your input graph was described (e.g. edges can go in different order and this will have an impact on the result if there are many).
However, it's guaranteed that it will find some path which has optimal length.
Your table seems to be wrong at E and F vertices. The parent vertex for E is D (AB->BD->DE = 3 + 4 + 2 = 9), so is for F.
It depends on the implementation of the relaxation function. For example, the algorithm described in the wikipedia uses strictly a less-than comparison: if alt < dist[v] so in this case (and all the implementations I've seen) the shortest path from A to D is A -> B -> D.
Why? Because (S = settled nodes and Q = queue of nodes, a pair of distance, parent):
A, so you get the S = {A:0} and Q = {B:3,A C:5,A D:9,A} Q select B and relax it. You get S = {A:0 B:3,A} and Q = {C:(5,A) D:7,B E:10,B}Q select C and relax it. You get S = {A:0 B:3,A C:5,A} and Q = {D:7,B E:10,B}.Q select D and you can finish the algorithm.Note that in step 3, you don't need to change the parent of D because the new path is not better than the current path. If the relaxation algorithm uses a less-than-or-equal comparison, then the result will be different.