3

I am warning you, this could be confusing, and the code i have written is more of a mindmap than finished code..

I am trying to implement the Newton-Raphson method to solve equations. What I can't figure out is how to write this

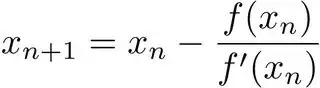
enter image description here

equation in Python, to calculate the next approximation (xn+1) from the last approximation (xn). I have to use a loop, to get closer and closer to the real answer, and the loop should terminate when the change between approximations is less than the variable h.

  1. How do I write the code for the equation?

  2. How do I terminate the loop when the approximations are not changing anymore?

    Calculates the derivative for equation f, in point x, with the accuracy h (this is used in the equation for solve())

    def derivative(f, x, h):
    deriv = (1.0/(2*h))*(f(x+h)-f(x-h))
    return deriv

    The numerical equation solver

    Supposed to loop until the difference between approximations is less than h

    def solve(f, x0, h):
    xn = x0
    prev = 0

    while ( approx - prev > h):
         xn = xn - (f(xn))/derivative(f, xn, h)

    return xn
Hooked
  • 84,485
  • 43
  • 192
  • 261
user2906011
  • 129
  • 2
  • 3
  • 7
  • Is the equation that you're solving for given? Because otherwise you can't write the equation. Once you have it, implement it as `def f(x):` etc. - just another function definition. And you need to take the _absolute value_ of the difference to test for the end of the loop (after which your `solve` function will return). – Floris Dec 18 '13 at 13:32
  • @Floris Netwon-Raphson's method finds the zero of the function (solves the equation `f(x)=0`) – Ramchandra Apte Dec 18 '13 at 13:33
  • I know but you need to know what f is… he asked "how do I write the code for the equation". – Floris Dec 18 '13 at 13:33

4 Answers4

7

Here is the implementation of a N-R solver expanding what you wrote above (complete, working). I added a few extra lines to show what is happening...

def derivative(f, x, h):
      return (f(x+h) - f(x-h)) / (2.0*h)  # might want to return a small non-zero if ==0

def quadratic(x):
    return 2*x*x-5*x+1     # just a function to show it works

def solve(f, x0, h):
    lastX = x0
    nextX = lastX + 10* h  # "different than lastX so loop starts OK
    while (abs(lastX - nextX) > h):  # this is how you terminate the loop - note use of abs()
        newY = f(nextX)                     # just for debug... see what happens
        print "f(", nextX, ") = ", newY     # print out progress... again just debug
        lastX = nextX
        nextX = lastX - newY / derivative(f, lastX, h)  # update estimate using N-R
    return nextX

xFound = solve(quadratic, 5, 0.01)    # call the solver
print "solution: x = ", xFound        # print the result

output:

f( 5.1 ) =  27.52
f( 3.31298701299 ) =  6.38683083151
f( 2.53900845771 ) =  1.19808560807
f( 2.30664271935 ) =  0.107987672721
f( 2.28109300639 ) =  0.00130557566462
solution: x =  2.28077645501

Edit - you could also check the value of newY and stop when it is "close enough to zero" - but usually you keep this going until the change in x is <=h (you can argue about the value of the = sign in a numerical method - I prefer the more emphatic < myself, figuring that one more iteration won't hurt.).

Floris
  • 45,857
  • 6
  • 70
  • 122
  • 1
    I always come here when I have to write the N-R from scratch. Three additions: if `derivative` is an internal function and `h` is an internal variable (and possibly a much smaller value) the full solver is contained within a single function. Also, check for `ZeroDivisionError` when calculating nextX – jake77 Mar 02 '18 at 12:02
2

If code under 'try:' cannot be implemented and the compiler is given the error 'ZeroDivisionError' then it will execute the code under 'except ZeroDivisionError:'. Although, if you'd like to account for another compiler exception 'XYZ' with a specific code implementation then add an additional 'except XYZ:"

 try:
    nextX = lastX - newY / derivative(function, lastX, h)
 except ZeroDivisionError:
    return newY
74U n3U7r1no
  • 309
  • 1
  • 13
  • If you could elaborate, explain what the code does in real words, it would be appreciated :) – Lea Cohen Jan 22 '15 at 06:49
  • (An edit has been made.) Pretty much if the compiler throws the 'ZeroDivisionError' exception because it failed to divide a number by zero then instead it will implement code under 'except ZeroDivisionError:' which in this case returns the value of newY because it couldn't be divided by zero. – 74U n3U7r1no Jan 24 '15 at 00:18
0

You'll be lucky to get convergence since your derivative is not exact to the limits of numerical precision.

Aside from your not guarding against division by zero, there's nothing wrong with your implementation of the Newton-Raphson result: that is your statement xn = xn - (f(xn))/derivative(f, xn, h)

But since you're using an approximate derivative, you should switch to a different optimisation scheme once you have the root bracketed. So as far as the Newton Raphson part is concerned, that is your termination condition. A good optimiser to use is brent which will always find a root once bracketed; even without a derivative.

Bathsheba
  • 231,907
  • 34
  • 361
  • 483
0

How do I write the code for the equation?

The Newton-Raphson method actually finds the zeroes of a function. To solve an equation g(x) = y, one has to make the function passed to the solver g(x)-y so that when the function passed to the solver gives zero, g(x)=y.

How do I terminate the loop when the approximations are not changing anymore?

Your code already does that as when the two approximations are equal to each other, the difference will be 0, which is less than h.

current_approx - previous_approx > h should be current_approx - previous_approx >= h since you want it to terminate when the difference is less than h. Also improved the variable names.

def derivative(f, x, accuracy):
    deriv = (1.0/(2*accuracy))*(f(x+accuracy)-f(x-accuracy))
    return deriv

def solve(f, approximation, h):
    current_approx = approximation
    prev_approximation = float("inf") # So that the first time the while loop will run

    while current_approx - prev_approx >= h:
        prev_approximation = current_approx
        current_approx = current_approx - (f(current_approx))/derivative(f, current_approx, h)

    return current_approx
Ramchandra Apte
  • 4,033
  • 2
  • 24
  • 44
  • Thank you! "The Newton-Raphson method actually finds the zeroes of a function. To solve an equation g(x) = y, one has to make the function passed to the solver g(x)-y so that when the function passed to the solver gives zero, g(x)=y." This was my next problem when trying to test my solve() method. How do you mean g(x)-y ? – user2906011 Dec 18 '13 at 14:05
  • @user2906011 That means if you have an equation, say `x^2 = 4`, then to solve it one would have to pass a function returning `x^2-4` because the Newton-Raphson solver finds `x` such that the function gives `0`. If `x^2-4=0`, then `x^2=4`, so a solution to the function is a solution to the equation. – Ramchandra Apte Dec 18 '13 at 14:09
  • So if I am trying to test it on say x^2-1=0, and 2^x-1=0 it should work? – user2906011 Dec 18 '13 at 14:19
  • @user2906011 For `x^2-1=0`, simply pass a function returning `x^2-1` to the solver. – Ramchandra Apte Dec 18 '13 at 14:20
  • That's what I did earlier... I added a print statement inside the while-loop, just to check if the loop even runs, and it doesn't. Is the problem: prev_approximation = float("inf") while current_approx - prev_approximation >= h: because current_approx minus an infinite number shouldn't be bigger than h right? – user2906011 Dec 18 '13 at 14:38