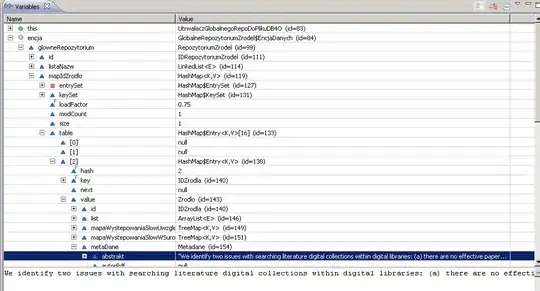
I'm sorry for the somewhat confusing title, but I wasn't sure how to sum this up any clearer.
I have two sets of X,Y data, each set corresponding to a general overall value. They are fairly densely sampled from the raw data. What I'm looking for is a way to find an interpolated X for any given Y for a value in between the sets I already have.
The graph makes this more clear:
In this case, the red line is from a set corresponding to 100, the yellow line is from a set corresponding to 50.
I want to be able to say, assuming these sets correspond to a gradient of values (even though they are clearly made up of discrete X,Y measurements), how do I find, say, where the X would be if the Y was 500 for a set that corresponded to a value of 75?
In the example here I would expect my desired point to be somewhere around here:
I do not need this function to be overly fancy — it can be simple linear interpolation of data points. I'm just having trouble thinking it through.
Note that neither the Xs nor the Ys of the two sets overlap perfectly. However it is rather trivial to say, "where are the nearest X points these sets share," or "where are the nearest Y points these sets share."
I have used simple interpolation between known values (e.g. find the X for corresponding Ys for set "50" and "100", then average those to get "75") and I end up with something like that looks like this:
So clearly I am doing something wrong here. Obviously in this case X is (correctly) returning as 0 for all of those cases where the Y is higher than the maximum Y of the "lowest" set. Things start out great but somewhere around when one starts to approach the maximum Y for the lowest set it starts going haywire.
It's easy to see why mine is going wrong. Here's another way to look at the problem:
In the "correct" version, X ought to be about 250. Instead, what I'm doing is essentially averaging 400 and 0 so X is 200. How do I solve for X in such a situation? I was thinking that bilinear interpolation might hold the answer but nothing I've been able to find on that has made it clear how I'd go about this sort of thing, because they all seem to be structured for somewhat different problems.
Thank you for your help. Note that while I have obviously graphed the above data in R to make it easy to see what I'm talking about, the final work for this is in Javascript and PHP. I'm not looking for something heavy duty; simple is better.