How to implement B+ tree in Haskell?

Question

A B+ tree has the leaf nodes linked together. Viewing the pointer structure of a B+ tree as directed graph its not cyclic. But ignoring the directions of pointers and viewing it as undirected the leaf nodes linked together creates cycles in the graph.

In Haskell how could a leaf be constructed as the child of a parent internal node and simultaneously the next link from the adjacent leaf node. How could one do this with Haskell's algebraic datatypes? It seems that Haskell ADT in general make cyclic like structures difficult to express.

Assuming you want mutable B+ tress, for the "links" you would use an IORef/MVar/TVar/etc to construct the "links". And then the process looks just like other languages. — Chris Kuklewicz, Dec 01 '13 at 10:03
Matthew Brecknell made a video that explains the creation of a B-tree using GADT's that you can at http://matthew.brecknell.net/post/btree-gadt/ . It's not exactly what you want but should be a good starting point. — Varun Madiath, Dec 03 '13 at 21:12

score 15 · Answer 1 · edited Feb 08 '17 at 14:49

Here is an idea for (immutable / "mutable"-by-reconstruction / zipperable) ADT representation (involving immutable vectors):

module Data.BTree.Internal where

import Data.Vector

type Values v = Vector v

type Keys k = Vector k

data Leaf k v
  = Leaf
    { _leafKeys   :: !(Keys k)
    , _leafValues :: !(Values v)
    , _leafNext   :: !(Maybe (Leaf k v)) -- @Maybe@ is lazy in @Just@, so this strict mark
                                         -- is ok for tying-the-knot stuff.
    -- , _leafPrev   :: !(Maybe (Leaf k v))
    -- ^ for doubly-linked lists of leaves
    }

type Childs k v = Vector (BTree k v)

data Node k v
  = Node
    { _nodeKeys   :: !(Keys k)
    , _nodeChilds :: !(Childs k v)
    }

data BTree k v
  = BTreeNode !(Node k v)
  | BTreeLeaf !(Leaf k v)

newtype BTreeRoot k v
  = BTreeRoot (BTree k v)

This should be internal, so that improper usage of raw constructors, accessors or pattern-matching wouldn't break the tree.
Keys, Values, Childs length control can be added (with run-time checks or possibly with GADTs and such).

And for an interface:

module Data.BTree ( {- appropriate exports -} ) where

import Data.Vector
import Data.BTree.Internal

-- * Building trees: "good" constructors.

keys :: [k] -> Keys k
keys = fromList

values :: [v] -> Values v
values = fromList

leaves :: [Leaf k v] -> Childs k v
leaves = fromList . fmap BTreeLeaf

leaf :: Keys k -> Values v -> Maybe (Leaf k v) -> Leaf k v
-- or
-- leaf :: Keys k -> Values v -> Maybe (Leaf k v) -> Maybe (Leaf k v) -> Leaf k v
-- for doubly-linked lists of leaves
leaf = Leaf

node :: Keys k -> Childs k v -> BTree k v
node ks = BTreeNode . Node ks

-- ...

-- * "Good" accessors.

-- ...

-- * Basic functions: insert, lookup, etc.

-- ...

Then this kind of a tree:

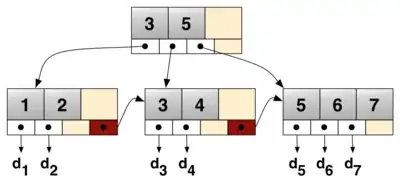
B+tree example

can be built as

test :: BTree Int ByteString
test = let
  root  = node (keys [3, 5]) (leaves [leaf1, leaf2, leaf3])
  leaf1 = leaf (keys [1, 2]) (values ["d1", "d2"]) (Just leaf2)
  leaf2 = leaf (keys [3, 4]) (values ["d3", "d4"]) (Just leaf3)
  leaf3 = leaf (keys [5, 6, 7]) (values ["d5", "d6", "d7"]) Nothing
  in root

This technique known as "tying the knot". Leaves can be cycled:

  leaf1 = leaf (keys [1, 2]) (values ["d1", "d2"]) (Just leaf2)
  leaf2 = leaf (keys [3, 4]) (values ["d3", "d4"]) (Just leaf3)
  leaf3 = leaf (keys [5, 6, 7]) (values ["d5", "d6", "d7"]) (Just leaf1)

or doubly-linked (assuming _leafPrev and corresponding leaf function):

  leaf1 = leaf (keys [1, 2]) (values ["d1", "d2"]) (Just leaf2) (Just leaf3)
  leaf2 = leaf (keys [3, 4]) (values ["d3", "d4"]) (Just leaf3) (Just leaf1)
  leaf3 = leaf (keys [5, 6, 7]) (values ["d5", "d6", "d7"]) (Just leaf1) (Just leaf2)

Fully mutable representation is also possible with mutable vectors and mutable references:

type Values v = IOVector v

type Keys k = IOVector k

type Childs k v = IOVector (BTree k v)

    , _leafNext   :: !(IORef (Maybe (Leaf k v)))

and so on, basically the same, but using IORef and IOVector, working in IO monad.

But can the immutable approach be made to work with for example insertion operations? — user782220, Dec 07 '13 at 11:29
@user782220 `insert` should be a function with signature `Ord k => k -> v -> BTreeRoot k v -> BTreeRoot k v` (takes an "old" tree and returns a "new"), the question is how many data can be shared between old and new trees (it is common to share data between immutable structures), with simple B trees it is possible to share unaffected sub-trees, but if the leaves is linked, then the whole tree should be reconstructed again. It can be fixed by making the links mutable (`!(IORef (Maybe (Leaf k v)))`), leaving vectors immutable (or not, depending on other possible issues (e.g. redistribution)). — JJJ, Dec 08 '13 at 11:45
@JJJ: Haskell noob. Is it possible to use `newtype` for `Keys` and `Values` instead of `type`? What are the advantages/disadvantages? — Ralph, Apr 16 '17 at 12:40

score 2 · Answer 2 · answered Dec 01 '13 at 21:57

Perhaps this is similar to what you are looking for?

data Node key value
    = Empty
    | Internal key [Node key value] -- key and children
    | Leaf value (Node key value) -- value and next-leaf
    deriving Show

let a = Leaf 0 b
    b = Leaf 1 c
    c = Leaf 2 d
    d = Leaf 3 Empty
in  Internal [Internal 0 [a,b], Internal 2 [c,d]]

An issue with this definition is that it does not prevent the next-leaf in a Leaf node from being an Internal node.

It is actually easy to make cyclic structures with Haskell, even infinite ones. For example, the following is an infinite list of zeroes, which is cyclic.

let a = 0:a

You can even do mutual recursion, which is even more cyclic:

let a = 0:b
    b = 1:a
in  a

By the way, this is a multiway tree, not a B+ tree. Also, this does not prevent us from putting any invalid value into the next-leaf argument in the Leaf constructor. — edom, Dec 04 '13 at 20:15

How to implement B+ tree in Haskell?

2 Answers2