Collision Detection between Accelerating Spheres

Question

I am writing a physics engine/simulator which incorporates 3D space flight, planetary/stellar gravitation, ship thrust and relativistic effects. So far, it is going very well, however, one thing that I need help with is the math of the collision detection algorithm.

The iterative simulation of movement that I am using is basically as follows:

(Note: 3D Vectors are ALL CAPS.)

For each obj

    obj.ACC = Sum(all acceleration influences)

    obj.POS = obj.POS + (obj.VEL * dT) + (obj.ACC * dT^2)/2     (*EQ.2*)

    obj.VEL = obj.VEL + (obj.ACC * dT)

Next

Where:

obj.ACC is the acceleration vector of the object
obj.POS is the position or location vector of the object
obj.VEL is the velocity vector of the object

obj.Radius is the radius (scalar) of the object

dT is the time delta or increment

What I basically need to do is to find some efficient formula that derives from (EQ.2) above for two objects (obj1, obj2) and tell if they ever collide, and if so, at what time. I need the exact time both so that I can determine if it is in this particular time increment (because acceleration will be different at different time increments) and also so that I can locate the exact position (which I know how to do, given the time)

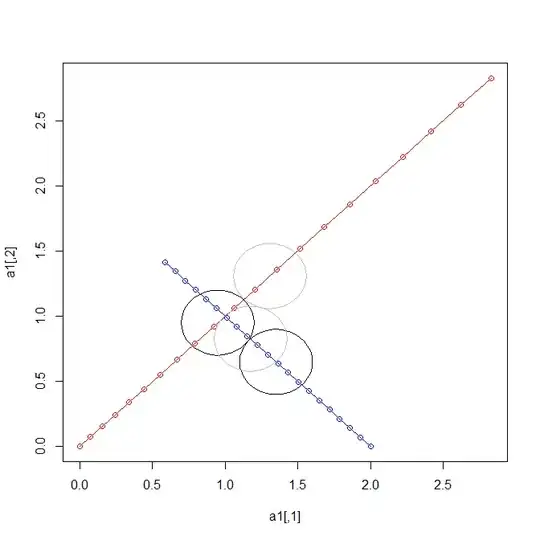
For this engine, I am modelling all objects as spheres, all this formula/algorithm needs to do is to figure out at what points:

(obj1.POS - obj2.POS).Distance = (obj1.Radius + obj2.Radius)

where .Distance is a positive scalar value. (You can also square both sides if this is easier, to avoid the square root function implicit in the .Distance calculation).

(yes, I am aware of many, many other collision detection questions, however, their solutions all seem to be very particular to their engine and assumptions, and none appear to match my conditions: 3D, spheres, and acceleration applied within the simulation increments. Let me know if I am wrong.)

---

Some Clarifications:

1) It is not sufficient for me to check for Intersection of the two spheres before and after the time increment. In many cases their velocities and position changes will far exceed their radii.

2) RE: efficiency, I do not need help (at this point anyway) with respect to determine likely candidates for collisions, I think that I have that covered.

---

Another clarification, which seems to be coming up a lot:

3) My equation (EQ.2) of incremental movement is a quadratic equation that applies both Velocity and Acceleration:

obj.POS = obj.POS + (obj.VEL * dT) + (obj.ACC * dT^2)/2

In the physics engines that I have seen, (and certainly every game engine that I ever heard of) only linear equations of incremental movement that apply only Velocity:

obj.POS = obj.POS + (obj.VEL * dT)

This is why I cannot use the commonly published solutions for collision detection found on StackOverflow, on Wikipedia and all over the Web, such as finding the intersection/closest approach of two line segments. My simulation deals with variable accelerations that are fundamental to the results, so what I need is the intersection/closest approach of two parabolic segments.

Answer 1

On the webpage AShelley referred to, the Closest Point of Approach method is developed for the case of two objects moving at constant velocity. However, I believe the same vector-calculus method can be used to derive a result in the case of two objects both moving with constant non-zero acceleration (quadratic time dependence).

In this case, the time derivative of the distance-squared function is 3rd order (cubic) instead of 1st order. Therefore there will be 3 solutions to the Time of Closest Approach, which is not surprising since the path of both objects is curved so multiple intersections are possible. For this application, you would probably want to use the earliest value of t which is within the interval defined by the current simulation step (if such a time exists).

I worked out the derivative equation which should give the times of closest approach:

0 = |D_ACC|^2 * t^3 + 3 * dot(D_ACC, D_VEL) * t^2 + 2 * [ |D_VEL|^2 + dot(D_POS, D_ACC) ] * t + 2 * dot(D_POS, D_VEL)

where:

D_ACC = ob1.ACC-obj2.ACC

D_VEL = ob1.VEL-obj2.VEL (before update)

D_POS = ob1.POS-obj2.POS (also before update)

and dot(A, B) = A.x*B.x + A.y*B.y + A.z*B.z

(Note that the square of the magnitude |A|^2 can be computed using dot(A, A))

To solve this for t, you'll probably need to use formulas like the ones found on Wikipedia.

Of course, this will only give you the moment of closest approach. You will need to test the distance at this moment (using something like Eq. 2). If it is greater than (obj1.Radius + obj2.Radius), it can be disregarded (i.e. no collision). However, if the distance is less, that means the spheres collide before this moment. You could then use an iterative search to test the distance at earlier times. It might also be possible to come up with another (even more complicated) derivation which takes the size into account, or possible to find some other analytic solution, without resorting to iterative solving.

Edit: because of the higher order, some of the solutions to the equation are actually moments of farthest separation. I believe in all cases either 1 of the 3 solutions or 2 of the 3 solutions will be a time of farthest separation. You can test analytically whether you're at a min or a max by evaluating the second derivative with respect to time (at the values of t which you found by setting the first derivative to zero):

D''(t) = 3 * |D_ACC|^2 * t^2 + 6 * dot(D_ACC, D_VEL) * t + 2 * [ |D_VEL|^2 + dot(D_POS, D_ACC) ]

If the second derivative evaluates to a positive number, then you know the distance is at a minimum, not a maximum, for the given time t.

Answer 2

Draw a line between the start location and end location of each sphere. If the resulting line segments intersect the spheres definitely collided at some point and some clever math can find at what time the collision occurred. Also make sure to check if the minimum distance between the segments (if they don't intersect) is ever less than 2*radius. This will also indicate a collision.

From there you can backstep your delta time to happen exactly at collision so you can correctly calculate the forces.

Have you considered using a physics library which already does this work? Many libraries use far more advanced and more stable (better integrators) systems for solving the systems of equations you're working with. Bullet Physics comes to mind.

Answer 3

op asked for time of collision. A slightly different approach will compute it exactly...

Remember that the position projection equation is:

NEW_POS=POS+VEL*t+(ACC*t^2)/2

If we replace POS with D_POS=POS_A-POS_B, VEL with D_VEL=VEL_A-VEL_B, and ACC=ACC_A-ACC_B for objects A and B we get:

$D_NEW_POS=D_POS+D_VEL*t+(D_ACC*t^2)/2

This is the formula for vectored distance between the objects. In order to get the squared scalar distance between them, we can take the square of this equation, which after expansion looks like:

distsq(t) = D_POS^2+2*dot(D_POS,D_VEL)*t + (dot(D_POS, D_ACC)+D_VEL^2)*t^2 + dot(D_VEL,D_ACC)*t^3 + D_ACC^2*t^4/4

In order to find the time where collision occurs, we can set the equation equal to the square of the sum of radii and solve for t:

0 = D_POS^2-(r_A+r_B)^2 + 2*dot(D_POS,D_VEL)*t + (dot(D_POS, D_ACC)+D_VEL^2)*t^2 + dot(D_VEL,D_ACC)*t^3 + D_ACC^2*t^4/4

Now, we can solve for the equation using the quartic formula.

The quartic formula will yield 4 roots, but we are only interested in real roots. If there is a double real root, then the two objects touch edges at exactly one point in time. If there are two real roots, then the objects continuously overlap between root 1 and root 2 (i.e. root 1 is the time when collision starts and root 2 is the time when collision stops). Four real roots means that the objects collide twice, continuously between root pairs 1,2 and 3,4.

In R, I used polyroot() to solve as follows:

# initial positions
POS_A=matrix(c(0,0),2,1)
POS_B=matrix(c(2,0),2,1)
# initial velocities
VEL_A=matrix(c(sqrt(2)/2,sqrt(2)/2),2,1)
VEL_B=matrix(c(-sqrt(2)/2,sqrt(2)/2),2,1)
# acceleration
ACC_A=matrix(c(sqrt(2)/2,sqrt(2)/2),2,1)
ACC_B=matrix(c(0,0),2,1)
# radii
r_A=.25
r_B=.25
# deltas
D_POS=POS_B-POS_A
D_VEL=VEL_B-VEL_A
D_ACC=ACC_B-ACC_A


# quartic coefficients
z=c(t(D_POS)%*%D_POS-r*r, 2*t(D_POS)%*%D_VEL, t(D_VEL)%*%D_VEL+t(D_POS)%*%D_ACC, t(D_ACC)%*%D_VEL, .25*(t(D_ACC)%*%D_ACC))
# get roots
roots=polyroot(z)
# In this case there are only two real roots...
root1=as.numeric(roots[1])
root2=as.numeric(roots[2])

# trajectory over time
pos=function(p,v,a,t){
  T=t(matrix(t,length(t),2))
  return(t(matrix(p,2,length(t))+matrix(v,2,length(t))*T+.5*matrix(a,2,length(t))*T*T))
}

# plot A in red and B in blue
t=seq(0,2,by=.1) # from 0 to 2 seconds.
a1=pos(POS_A,VEL_A,ACC_A,t)
a2=pos(POS_B,VEL_B,ACC_B,t)
plot(a1,type='o',col='red')
lines(a2,type='o',col='blue')

# points of a circle with center 'p' and radius 'r'
circle=function(p,r,s=36){
  e=matrix(0,s+1,2)
  for(i in 1:s){
    e[i,1]=cos(2*pi*(1/s)*i)*r+p[1]
    e[i,2]=sin(2*pi*(1/s)*i)*r+p[2]
  }
  e[s+1,]=e[1,]
  return(e)
}

# plot circles with radius r_A and r_B at time of collision start in black
lines(circle(pos(POS_A,VEL_A,ACC_A,root1),r_A))
lines(circle(pos(POS_B,VEL_B,ACC_B,root1),r_B))
# plot circles with radius r_A and r_B at time of collision stop in gray
lines(circle(pos(POS_A,VEL_A,ACC_A,root2),r_A),col='gray')
lines(circle(pos(POS_B,VEL_B,ACC_B,root2),r_B),col='gray')

Object A follows the red trajectory from the lower left to the upper right. Object B follows the blue trajectory from the lower right to the upper left. The two objects collide continuously between time 0.9194381 and time 1.167549. The two black circles just touch, showing the beginning of overlap - and overlap continues in time until the objects reach the location of the gray circles.

Answer 4

Seems like you want the Closest Point of Approach (CPA). If it is less than the sum of the radiuses, you have a collision. There is example code in the link. You can calculate each frame with the current velocity, and check if the CPA time is less than your tick size. You could even cache the cpa time, and only update when acceleration was applied to either item.