Dijkstra's is typically used to find the shortest distance between two nodes in a graph. Can it be used to find a minimum spanning tree? If so, how?
Edit: This isn't homework, but I am trying to understand a question on an old practice exam.
Dijkstra's is typically used to find the shortest distance between two nodes in a graph. Can it be used to find a minimum spanning tree? If so, how?
Edit: This isn't homework, but I am trying to understand a question on an old practice exam.
The answer is no. To see why, let's first articulate the question like so:
G = (V, E, w) with only nonnegative edge weights, does the predecessor subgraph produced by Dijkstra's Algorithm form a minimum spanning tree of G?(Note that undirected graphs are a special class of directed graphs, so it is perfectly ok to use Dijkstra's Algorithm on undirected graphs. Furthermore, MST's are defined only for connected, undirected graphs, and are trivial if the graph is not weighted, so we must restrict our inquiry to these graphs.)
A: Dijkstra's Algorithm at every step greedily selects the next edge that is closest to some source vertex s. It does this until s is connected to every other vertex in the graph. Clearly, the predecessor subgraph that is produced is a spanning tree of G, but is the sum of edge weights minimized?
Prim's Algorithm, which is known to produce a minimum spanning tree, is highly similar to Dijkstra's Algorithm, but at each stage it greedily selects the next edge that is closest to any vertex currently in the working MST at that stage. Let's use this observation to produce a counterexample.
Counterexample: Consider the undirected graph G = (V, E, w) where
V = { a, b, c, d }
E = { (a,b), (a,c), (a,d), (b,d), (c,d) }
w = {
( (a,b) , 5 )
( (a,c) , 5 )
( (a,d) , 5 )
( (b,d) , 1 )
( (c,d) , 1 )
}
Take a as the source vertex.

Dijkstra's Algorithm takes edges { (a,b), (a,c), (a,d) }.
Thus, the total weight of this spanning tree is 5 + 5 + 5 = 15.
Prim's Algorithm takes edges { (a,d), (b,d), (c,d) }.
Thus, the total weight of this spanning tree is 5 + 1 + 1 = 7.
Strictly, the answer is no. Dijkstra's algorithm finds the shortest path between 2 vertices on a graph. However, a very small change to the algorithm produces another algorithm which does efficiently produce an MST.
The Algorithm Design Manual is the best book I've found to answer questions like this one.
I'd keep to a greedy algorithm such as Prim's or Kruskal's. I fear Djikstra's won't do, simply because it minimizes the cost between pairs of nodes, not for the whole tree.
Of course, It's possible to use Dijkstra for minimum spanning tree:
dijsktra(s):
dist[s] = 0;
while (some vertices are unmarked) {
v = unmarked vertex with
smallest dist;
Mark v; // v leaves “table”
for (each w adj to v) {
dist[w] = min[ dist[w], dist[v] + c(v,w) ];
}
}
Here is an example of using Dijkstra for spanning tree:
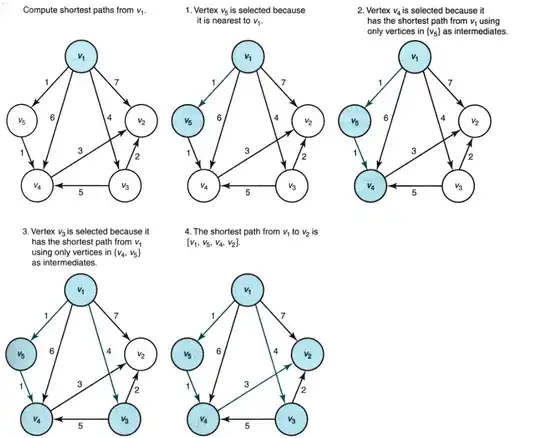
You can find further explanation in Foundations of Algorithms book, chapter 4, section 2.
Hope this help