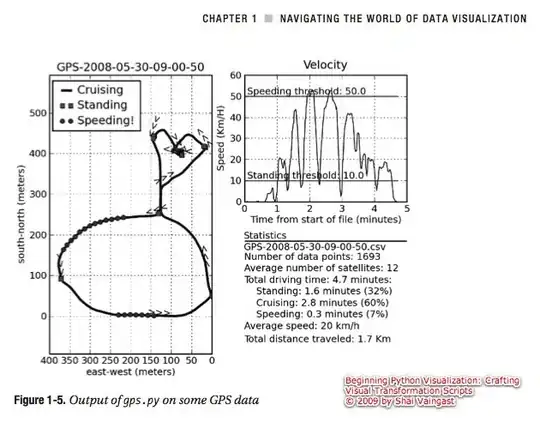
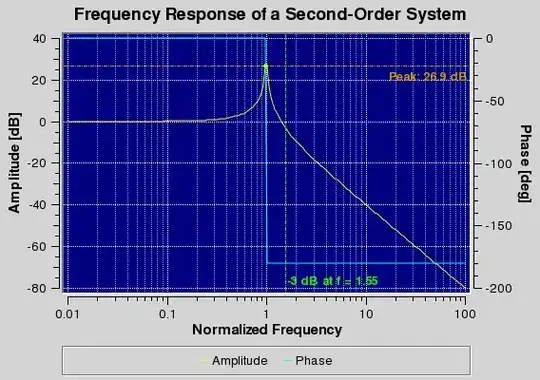
For example, I would like to map the colour to z, with 0 maps to "white".
> a <- data.frame(x=1:10, y=1, z=c(rnorm(8),-12,12))
> a
x y z
1 1 1 -0.4603911
2 2 1 -0.4868471
3 3 1 0.2180346
4 4 1 -0.8807652
5 5 1 1.7379462
6 6 1 -0.1334904
7 7 1 -0.3675578
8 8 1 0.9225425
9 9 1 -12.0000000
10 10 1 12.0000000
ggplot(a,aes(x=x,y=y,fill=z)) + geom_bar(stat="identity") +
scale_fill_gradient2(high="green", mid="white", low="red")
As you can see the colour is not really useful indicator, instead of conveying a general idea of how the values are distributed, now the colour only tells which values are extreme, leaving the majority values indistinguishable by untrained eyes.
There is a method Non-linear color distribution over the range of values in a geom_raster but it seems a bit complicated and I can only vaguely understand how it works.
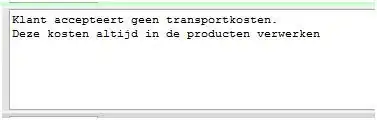
I then thought maybe order is a good rescale way, hence:
ggplot(a,aes(x=x,y=y,fill=ecdf(z)(z))) + geom_bar(stat="identity") +
scale_fill_gradient2(high="green", mid="white", low="red", midpoint=ecdf(a$z)(0))
It worked to some extent (here I used ecdf instead of order to find what value 0 is rescaled. However, the drawback is, I would like to keep the labels of the legend as the unscaled values, instead of the rescaled ones. So something like labels=function(x) quantile(a$z, x), which I cannot make it work. Also, I find it stupid to repeatedly using ecdf and quantile to rescale forward and backward.
Is there any better or simpler approach in these cases, e.g. robust (not need to be optimal or very accurate) enough to fill reasonable colours for all kinds of distributions of mapped values.