Angle between two vectors in R

Question

What the most efficient way in the programming language R to calculate the angle between two vectors?

Answer 1

According to page 5 of this PDF, sum(a*b) is the R command to find the dot product of vectors a and b, and sqrt(sum(a * a)) is the R command to find the norm of vector a, and acos(x) is the R command for the arc-cosine. It follows that the R code to calculate the angle between the two vectors is

theta <- acos( sum(a*b) / ( sqrt(sum(a * a)) * sqrt(sum(b * b)) ) )

Answer 2

My answer consists of two parts. Part 1 is the math - to give clarity to all readers of the thread and to make the R code that follows understandable. Part 2 is the R programming.

Part 1 - Math

The dot product of two vectors x and y can be defined as:

where ||x|| is the Euclidean norm (also known as the L₂ norm) of the vector x.

Manipulating the definition of the dot product, we can obtain:

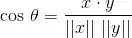
where theta is the angle between the vectors x and y expressed in radians. Note that theta can take on a value that lies on the closed interval from 0 to pi.

Solving for theta itself, we get:

Part 2 - R Code

To translate the mathematics into R code, we need to know how to perform two matrix (vector) calculations; dot product and Euclidean norm (which is a specific type of norm, known as the L₂ norm). We also need to know the R equivalent of the inverse cosine function, cos^-1.

Starting from the top. By reference to ?"%*%", the dot product (also referred to as the inner product) can be calculated using the %*% operator. With reference to ?norm, the norm() function (base package) returns a norm of a vector. The norm of interest here is the L₂ norm or, in the parlance of the R help documentation, the "spectral" or "2"-norm. This means that the type argument of the norm() function ought to be set equal to "2". Lastly, the inverse cosine function in R is represented by the acos() function.

Solution

Equipped with both the mathematics and the relevant R functions, a prototype function (that is, not production standard) can be put together - using Base package functions - as shown below. If the above information makes sense then the angle() function that follows should be clear without further comment.

angle <- function(x,y){
  dot.prod <- x%*%y 
  norm.x <- norm(x,type="2")
  norm.y <- norm(y,type="2")
  theta <- acos(dot.prod / (norm.x * norm.y))
  as.numeric(theta)
}

Test the function

A test to verify that the function works. Let x = (2,1) and y = (1,2). Dot product between x and y is 4. Euclidean norm of x is sqrt(5). Euclidean norm of y is also sqrt(5). cos theta = 4/5. Theta is approximately 0.643 radians.

x <- as.matrix(c(2,1))
y <- as.matrix(c(1,2))
angle(t(x),y)          # Use of transpose to make vectors (matrices) conformable.
[1] 0.6435011

I hope this helps!

Answer 3

For 2D-vectors, the way given in the accepted answer and other ones does not take into account the orientation (the sign) of the angle (angle(M,N) is the same as angle(N,M)) and it returns a correct value only for an angle between 0 and pi.

Use the atan2 function to get an oriented angle and a correct value (modulo 2pi).

angle <- function(M,N){
  acos( sum(M*N) / ( sqrt(sum(M*M)) * sqrt(sum(N*N)) ) )
}
angle2 <- function(M,N){
  atan2(N[2],N[1]) - atan2(M[2],M[1]) 
}

Check that angle2 gives the correct value:

> theta <- seq(-2*pi, 2*pi, length.out=10)
> O <- c(1,0)
> test1 <- sapply(theta, function(theta) angle(M=O, N=c(cos(theta),sin(theta))))
> all.equal(test1 %% (2*pi), theta %% (2*pi))
[1] "Mean relative difference: 1"
> test2 <- sapply(theta, function(theta) angle2(M=O, N=c(cos(theta),sin(theta))))
> all.equal(test2 %% (2*pi), theta %% (2*pi))
[1] TRUE

Answer 4

You should use the dot product. Say you have V₁ = (x₁, y₁, z₁) and V₂ = (x₂, y₂, z₂), then the dot product, which I'll denote by V₁·V₂, is calculated as

V₁·V₂ = x₁·x₂ + y₁·y₂ + z₁·z₂ = |V₁| · |V₂| · cos(θ);

What this means is that that sum shown on the left is equal to the product of the absolute values of the vectors times the cosine of the angle between the vectors. the absolute value of the vectors V₁ and V₂ are calculated as

|V₁| = √(x₁² + y₁² + z₁²), and
|V₂| = √(x₂² + y₂² + z₂²),

So, if you rearrange the first equation above, you get

cos(θ) = (x₁·x₂ + y₁·y₂ + z₁·z₂) ÷ (|V₁|·|V₂|),

and you just need the arccos function (or inverse cosine) applied to cos(θ) to get the angle.

Depending on your arccos function, the angle may be in degrees or radians.

(For two dimensional vectors, just forget the z-coordinates and do the same calculations.)

Good luck,

John Doner

Answer 5

if you install/upload the library(matlib): there is a function called angle(x, y, degree = TRUE) where x and y are vectors. Note: if you have x and y in matrix form, use as.vector(x) and as.vector(y):

library(matlib)
matA <- matrix(c(3, 1), nrow = 2)  ##column vectors
matB <- matrix(c(5, 5), nrow = 2)
angle(as.vector(matA), as.vector(matB))  
##default in degrees, use degree = FALSE for radians

Answer 6

Another solution : the correlation between the two vectors is equal to the cosine of the angle between two vectors.

so the angle can be computed by acos(cor(u,v))

# example u(1,2,0) ; v(0,2,1)

cor(c(1,2),c(2,1))
theta = acos(cor(c(1,2),c(2,1)))

Answer 7

The traditional approach to obtaining an angle between two vectors (i.e. acos(sum(a*b) / (sqrt(sum(a*a)) * sqrt(sum(b*b)))), as presented in some of the other answers) suffers from numerical instability in several corner cases. The following code works for n-dimensions and in all corner cases (it doesn't check for zero length vectors, but that's easy to add). See notes below.

# Get angle between two n-dimensional vectors
angle_btw <- function(v1, v2) {

  signbit <- function(x) {
    x < 0
  }

  u1 <- v1 / norm(v1, "2")
  u2 <- v2 / norm(v2, "2")

  y <- u1 - u2
  x <- u1 + u2

  a0 <- 2 * atan(norm(y, "2") / norm(x, "2"))

  if (!(signbit(a0) || signbit(pi - a0))) {
    a <- a0
  } else if (signbit(a0)) {
    a <- 0.0
  } else {
    a <- pi
  }

  a
}

This code is adapted from a Julia implementation by Jeffrey Sarnoff (MIT license), in turn based on these notes by Prof. W. Kahan (page 15).

Answer 8

I think what you need is an inner product. For two vectors v,u (in R^n or any other inner-product spaces) <v,u>/|v||u|= cos(alpha). (were alpha is the angle between the vectors)

for more details see:

http://en.wikipedia.org/wiki/Inner_product_space

Answer 9

If you want to calculate the angle among multiple variables, you can use the following function, which is an extension of the solution provided by @Graeme Walsh.

angles <- function(matrix){

  ## Calculate the cross-product of the matrix
  cross.product <- t(matrix)%*%matrix

  ## the lower and the upper triangle of the cross-product is the dot products among vectors 
  dot.products<- cross.product[lower.tri(cross.product)]

  ## Calculate the L2 norms
  temp <- suppressWarnings(diag(sqrt(cross.product)))
  temp <- temp%*%t(temp)
  L2.norms <- temp[lower.tri(temp)]

  ## Arccosine values for each pair of variables
  lower.t <- acos(dot.products/L2.norms)

  ## Create an empty matrix to present the results
  result.matrix <- matrix(NA,ncol = dim(matrix)[2],nrow=dim(matrix)[2])

  ## Fill the matrix with arccosine values and assign the diagonal values as zero “0”
  result.matrix[lower.tri(result.matrix)] <- lower.t
  diag(result.matrix) <- 0
  result.matrix[upper.tri(result.matrix)] <- t(result.matrix)[upper.tri(t(result.matrix))]

  ## Get the result matrix
  return(result.matrix)
}

In addition, if you mean-centered your input variables and get the cosine values of the result matrix provided above, you will get the exact correlation matrix of the variables.

Here is an application of the function.

set.seed(123)
n <- 100
m <- 5

# Generate a set of random variables 

mt <- matrix(rnorm(n*m),nrow = n,ncol = m)

# Mean-centered matrix
mt.c <- scale(mt,scale = F)

# Cosine angles 
cosine.angles <- angles(matrix = mt)

> cosine.angles
         [,1]     [,2]     [,3]     [,4]     [,5]
[1,] 0.000000 1.630819 1.686037 1.618119 1.751859
[2,] 1.630819 0.000000 1.554695 1.523353 1.712214
[3,] 1.686037 1.554695 0.000000 1.619723 1.581786
[4,] 1.618119 1.523353 1.619723 0.000000 1.593681
[5,] 1.751859 1.712214 1.581786 1.593681 0.000000



# Centered-data cosine angles 
centered.cosine.angles <- angles(matrix = mt.c)

> centered.cosine.angles
         [,1]     [,2]     [,3]     [,4]     [,5]
[1,] 0.000000 1.620349 1.700334 1.614890 1.764721
[2,] 1.620349 0.000000 1.540213 1.526950 1.701793
[3,] 1.700334 1.540213 0.000000 1.615677 1.595647
[4,] 1.614890 1.526950 1.615677 0.000000 1.590057
[5,] 1.764721 1.701793 1.595647 1.590057 0.000000

# This will give you correlation matrix 
cos(angles(matrix = mt.c))

            [,1]        [,2]        [,3]        [,4]        [,5]
[1,]  1.00000000 -0.04953215 -0.12917601 -0.04407900 -0.19271110
[2,] -0.04953215  1.00000000  0.03057903  0.04383271 -0.13062219
[3,] -0.12917601  0.03057903  1.00000000 -0.04486571 -0.02484838
[4,] -0.04407900  0.04383271 -0.04486571  1.00000000 -0.01925986
[5,] -0.19271110 -0.13062219 -0.02484838 -0.01925986  1.00000000

# Orginal correlation matrix
cor(mt)

            [,1]        [,2]        [,3]        [,4]        [,5]
[1,]  1.00000000 -0.04953215 -0.12917601 -0.04407900 -0.19271110
[2,] -0.04953215  1.00000000  0.03057903  0.04383271 -0.13062219
[3,] -0.12917601  0.03057903  1.00000000 -0.04486571 -0.02484838
[4,] -0.04407900  0.04383271 -0.04486571  1.00000000 -0.01925986
[5,] -0.19271110 -0.13062219 -0.02484838 -0.01925986  1.00000000

# Check whether they are equal
all.equal(cos(angles(matrix = mt.c)),cor(mt))
[1] TRUE