How to calculate the number of coprime subsets of the set {1,2,3,..,n}

Question

I am solving this task (problem I). The statement is:

How many subsets of the set {1, 2, 3, ..., n} are coprime? A set of integers is called coprime if every two of its elements are coprime. Two integers are coprime if their greatest common divisor equals 1.

Input

First line of input contains two integers n and m (1 <= n <= 3000, 1 <= m <= 10^9 + 9)

Output

Output the number of coprime subsets of {1, 2, 3, ..., n} modulo m.

Example

input: 4 7 output: 5

There are 12 coprime subsets of {1,2,3,4}: {}, {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {3,4}, {1,2,3}, {1,3,4}.

---

I think it can be solved by using prime numbers. (keeping track of if we used each prime numbers) ..but I'm not sure.

Can I get some hints to solve this task?

• You can found this sequence at here : http://oeis.org/A084422

Answer 1

Okay, here’s the goods. The C program that follows gets n=3000 in less than 5 seconds for me. My hat’s off to the team(s) that solved this problem in a competitive setting.

The algorithm is based on the idea of treating the small and large primes differently. A prime is small if its square is at most n. Otherwise, it’s large. Observe that each number less than or equal to n has at most one large prime factor.

We make a table indexed by pairs. The first component of each pair specifies the number of large primes in use. The second component of each pair specifies the set of small primes in use. The value at a particular index is the number of solutions with that usage pattern not containing 1 or a large prime (we count those later by multiplying by the appropriate power of 2).

We iterate downward over numbers j with no large prime factors. At the beginning of each iteration, the table contains the counts for subsets of j..n. There are two additions in the inner loop. The first accounts for extending subsets by j itself, which does not increase the number of large primes in use. The second accounts for extending subsets by j times a large prime, which does. The number of suitable large primes is the number of large primes not greater than n/j, minus the number of large primes already in use, since the downward iteration implies that each large prime already in use is not greater than n/j.

At the end, we sum the table entries. Each subset counted in the table gives rise to 2 ** k subsets where k is one plus the number of unused large primes, as 1 and each unused large prime can be included or excluded independently.

/* assumes int, long are 32, 64 bits respectively */
#include <stdio.h>
#include <stdlib.h>

enum {
  NMAX = 3000
};

static int n;
static long m;
static unsigned smallfactors[NMAX + 1];
static int prime[NMAX - 1];
static int primecount;
static int smallprimecount;
static int largeprimefactor[NMAX + 1];
static int largeprimecount[NMAX + 1];
static long **table;

static void eratosthenes(void) {
  int i;
  for (i = 2; i * i <= n; i++) {
    int j;
    if (smallfactors[i]) continue;
    for (j = i; j <= n; j += i) smallfactors[j] |= 1U << primecount;
    prime[primecount++] = i;
  }
  smallprimecount = primecount;
  for (; i <= n; i++) {
    if (!smallfactors[i]) prime[primecount++] = i;
  }
  if (0) {
    int k;
    for (k = 0; k < primecount; k++) printf("%d\n", prime[k]);
  }
}

static void makelargeprimefactor(void) {
  int i;
  for (i = smallprimecount; i < primecount; i++) {
    int p = prime[i];
    int j;
    for (j = p; j <= n; j += p) largeprimefactor[j] = p;
  }
}

static void makelargeprimecount(void) {
  int i = 1;
  int j;
  for (j = primecount; j > smallprimecount; j--) {
    for (; i <= n / prime[j - 1]; i++) {
      largeprimecount[i] = j - smallprimecount;
    }
  }
  if (0) {
    for (i = 1; i <= n; i++) printf("%d %d\n", i, largeprimecount[i]);
  }
}

static void maketable(void) {
  int i;
  int j;
  table = calloc(smallprimecount + 1, sizeof *table);
  for (i = 0; i <= smallprimecount; i++) {
    table[i] = calloc(1U << smallprimecount, sizeof *table[i]);
  }
  table[0][0U] = 1L % m;
  for (j = n; j >= 2; j--) {
    int lpc = largeprimecount[j];
    unsigned sf = smallfactors[j];
    if (largeprimefactor[j]) continue;
    for (i = 0; i < smallprimecount; i++) {
      long *cur = table[i];
      long *next = table[i + 1];
      unsigned f;
      for (f = sf; f < (1U << smallprimecount); f = (f + 1U) | sf) {
        cur[f] = (cur[f] + cur[f & ~sf]) % m;
      }
      if (lpc - i <= 0) continue;
      for (f = sf; f < (1U << smallprimecount); f = (f + 1U) | sf) {
        next[f] = (next[f] + cur[f & ~sf] * (lpc - i)) % m;
      }
    }
  }
}

static long timesexp2mod(long x, int y) {
  long z = 2L % m;
  for (; y > 0; y >>= 1) {
    if (y & 1) x = (x * z) % m;
    z = (z * z) % m;
  }
  return x;
}

static long computetotal(void) {
  long total = 0L;
  int i;
  for (i = 0; i <= smallprimecount; i++) {
    unsigned f;
    for (f = 0U; f < (1U << smallprimecount); f++) {
      total = (total + timesexp2mod(table[i][f], largeprimecount[1] - i + 1)) % m;
    }
  }
  return total;
}

int main(void) {
  scanf("%d%ld", &n, &m);
  eratosthenes();
  makelargeprimefactor();
  makelargeprimecount();
  maketable();
  if (0) {
    int i;
    for (i = 0; i < 100; i++) {
      printf("%d %ld\n", i, timesexp2mod(1L, i));
    }
  }
  printf("%ld\n", computetotal());
  return EXIT_SUCCESS;
}

Answer 2

Here's an answer which goes through the first 200 elements in the sequence in less than a second, giving the right answer 200 → 374855124868136960. With optimizations (see edit 1), it can calculate the first 500 entries in under 90s, which is quick -- although @David Eisenstat's answer is likely to be better if it can be developed. I think takes a different approach to the algorithms given so far, including my own original answer, so I'm posting it separately.

After optimizing, I realized that I was really coding up a graph problem so I rewrote the solution as a graph implementation (see edit 2). The graph implementation allows some more optimizations, is a lot more elegant, more than an order of magnitude faster, and scales better: it calculates f(600) in 1.5s, compared to 27s.

The main idea here is to use a recursion relationship. For any set, the number of subsets meeting the criterion are the sum of:

• the number of subsets with one element removed; and
• the number of subsets with that element definitely included.

In the second case, when the element is definitely included, any other elements which aren't coprime with it must be removed.

Efficiency issues:

• I've chosen to remove the largest element to maximize the chance of that element already being coprime to all the others, in which case only one rather than two recursive calls need to be made.
• Caching / memoization helps.

Code below.

#include <cassert>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
#include <iostream>
#include <ctime>

const int PRIMES[] = // http://rlrr.drum-corps.net/misc/primes1.shtml
    { 2, 3, 5, ...
      ..., 2969, 2971, 2999 };
const int NPRIMES = sizeof(PRIMES) / sizeof(int);

typedef std::set<int> intset;
typedef std::vector<intset> intsetvec;

const int MAXCALC = 200; // answer at http://oeis.org/A084422/b084422.txt
intsetvec primeFactors(MAXCALC +1);

typedef std::vector<int> intvec;

// Caching / memoization
typedef std::map<intvec, double> intvec2dbl;
intvec2dbl set2NumCoPrimeSets;

double NumCoPrimeSets(const intvec& set)
{
    if (set.empty())
        return 1;

    // Caching / memoization
    const intvec2dbl::const_iterator i = set2NumCoPrimeSets.find(set);
    if (i != set2NumCoPrimeSets.end())
        return i->second;

    // Result is the number of coprime sets in:
    //      setA, the set that definitely has the first element of the input present
    // +    setB, the set the doesn't have the first element of the input present

    // Because setA definitely has the first element, we remove elements it isn't coprime with
    // We also remove the first element: as this is definitely present it doesn't make any
    // difference to the number of sets
    intvec setA(set);
    const int firstNum = *setA.begin();
    const intset& factors = primeFactors[firstNum];
    for(int factor : factors) {
        setA.erase(std::remove_if(setA.begin(), setA.end(),
            [factor] (int i) { return i % factor == 0; } ), setA.end());
    }

    // If the first element was already coprime with the rest, then we have setA = setB
    // and we can do a single call (m=2). Otherwise we have two recursive calls.
    double m = 1;
    double c = 0;
    assert(set.size() - setA.size() > 0);
    if (set.size() - setA.size() > 1) {
        intvec setB(set);
        setB.erase(setB.begin());
        c = NumCoPrimeSets(setB);
    }
    else {
        // first elt coprime with rest
        m = 2;
    }
    const double numCoPrimeSets = m * NumCoPrimeSets(setA) + c;

    // Caching / memoization
    set2NumCoPrimeSets.insert(intvec2dbl::value_type(set, numCoPrimeSets));
    return numCoPrimeSets;
}


int main(int argc, char* argv[])
{
    // Calculate prime numbers that factor into each number upto MAXCALC
    primeFactors[1].insert(1); // convenient
    for(int i=2; i<=MAXCALC; ++i) {
        for(int j=0; j<NPRIMES; ++j) {
            if (i % PRIMES[j] == 0) {
                primeFactors[i].insert(PRIMES[j]);
            }
        }
    }

    const clock_t start = clock();

    for(int n=1; n<=MAXCALC; ++n) {
        intvec v;
        for(int i=n; i>0; --i) { // reverse order to reduce recursion
            v.push_back(i);
        }
        const clock_t now = clock();
        const clock_t ms = now - start;
        const double numCoPrimeSubsets = NumCoPrimeSets(v);
        std::cout << n << ", " << std::fixed << numCoPrimeSubsets << ", " << ms << "\n";
    }

    return 0;
}

Time characteristics look a lot better than my first answer. But still won't go upto 3000 in 5s!

---

Edit 1

There are some interesting optimizations that can be made to this method. Overall this gives a 4x improvement for larger n.

• All numbers in the set that are already coprime can be removed in one single preprocessing step: if m number are removed, then the original set has 2^m factor times more combinations than the reduced one (because for each coprime, you can either have it in or out of the set independently of other elements).
• Most importantly, it is possible to choose an element to remove that is anywhere in the set. It turns out that removing the most connected element works best.
• The recursive relationship that was previously used can be generalized to remove more than one element where all elements removed have the same prime factors. E.g. for the set {2, 3, 15, 19, 45}, the numbers 15 and 45 have the same prime factors of 3 and 5. There are 2 numbers removed at once, and so the number of subsets for {2, 3, 15, 19, 45} = twice the number of combinations for either 15 or 45 present (for the set {2, 19} because 3 has to be absent if either 15 or 45 are present) + the number of subsets for 15 and 45 absent (for the set {2, 3, 19})
• Using short for the number type improved performance by about 10%.
• Finally, it is also possible to transform sets into sets with equivalent prime factors, in the hope of getting better cache hits by standardizing the sets. E.g., { 3, 9, 15} is equivalent (isomorphic) to 2, 4, 6. This was the most radical idea but probably had the least effect on performance.

It's probably a lot easier to understand it with a concrete example. I've chosen the set {1..12} which is large enough to get a feel for how it works but small enough so that it's comprehensible.

NumCoPrimeSets({ 1 2 3 4 5 6 7 8 9 10 11 12 })
Removed 3 coprimes, giving set { 2 3 4 5 6 8 9 10 12 } multiplication factor now 8
Removing the most connected number 12 with 8 connections
To get setA, remove all numbers which have *any* of the prime factors { 2 3 }
setA = { 5 }
To get setB, remove 2 numbers which have *exactly* the prime factors { 2 3 }
setB = { 2 3 4 5 8 9 10 }
**** Recursing on 2 * NumCoPrimeSets(setA) + NumCoPrimeSets(setB)

NumCoPrimeSets({ 5 })
Base case return the multiplier, which is 2
NumCoPrimeSets({ 2 3 4 5 8 9 10 })
Removing the most connected number 10 with 4 connections
To get setA, remove all numbers which have *any* of the prime factors { 2 5 }
setA = { 3 9 }
To get setB, remove 1 numbers which have *exactly* the prime factors { 2 5 }
setB = { 2 3 4 5 8 9 }
**** Recursing on 1 * NumCoPrimeSets(setA) + NumCoPrimeSets(setB)

NumCoPrimeSets({ 3 9 })
Transformed 2 primes, giving new set { 2 4 }
Removing the most connected number 4 with 1 connections
To get setA, remove all numbers which have *any* of the prime factors { 2 }
setA = { }
To get setB, remove 2 numbers which have *exactly* the prime factors { 2 }
setB = { }
**** Recursing on 2 * NumCoPrimeSets(setA) + NumCoPrimeSets(setB)

NumCoPrimeSets({ })
Base case return the multiplier, which is 1
NumCoPrimeSets({ })
Base case return the multiplier, which is 1
**** Returned from recursing on 2 * NumCoPrimeSets({ }) + NumCoPrimeSets({ })
Caching for{ 2 4 }: 3 = 2 * 1 + 1
Returning for{ 3 9 }: 3 = 1 * 3

NumCoPrimeSets({ 2 3 4 5 8 9 })
Removed 1 coprimes, giving set { 2 3 4 8 9 } multiplication factor now 2
Removing the most connected number 8 with 2 connections
To get setA, remove all numbers which have *any* of the prime factors { 2 }
setA = { 3 9 }
To get setB, remove 3 numbers which have *exactly* the prime factors { 2 }
setB = { 3 9 }
**** Recursing on 3 * NumCoPrimeSets(setA) + NumCoPrimeSets(setB)

NumCoPrimeSets({ 3 9 })
Transformed 2 primes, giving new set { 2 4 }
Cache hit, returning 3 = 1 * 3
NumCoPrimeSets({ 3 9 })
Transformed 2 primes, giving new set { 2 4 }
Cache hit, returning 3 = 1 * 3
**** Returned from recursing on 3 * NumCoPrimeSets({ 3 9 }) + NumCoPrimeSets({ 3 9 })
Caching for{ 2 3 4 8 9 }: 12 = 3 * 3 + 3
Returning for{ 2 3 4 5 8 9 }: 24 = 2 * 12

**** Returned from recursing on 1 * NumCoPrimeSets({ 3 9 }) + NumCoPrimeSets({ 2 3 4 5 8 9 })
Caching for{ 2 3 4 5 8 9 10 }: 27 = 1 * 3 + 24
Returning for{ 2 3 4 5 8 9 10 }: 27 = 1 * 27

**** Returned from recursing on 2 * NumCoPrimeSets({ 5 }) + NumCoPrimeSets({ 2 3 4 5 8 9 10 })
Caching for{ 2 3 4 5 6 8 9 10 12 }: 31 = 2 * 2 + 27
Returning for{ 1 2 3 4 5 6 7 8 9 10 11 12 }: 248 = 8 * 31

Code below

#include <cassert>
#include <vector>
#include <set>
#include <map>
#include <unordered_map>
#include <queue>
#include <algorithm>
#include <fstream>
#include <iostream>
#include <ctime>

typedef short numtype;

const numtype PRIMES[] = // http://rlrr.drum-corps.net/misc/primes1.shtml
    ...
const numtype NPRIMES = sizeof(PRIMES) / sizeof(numtype);

typedef std::set<numtype> numset;
typedef std::vector<numset> numsetvec;

const numtype MAXCALC = 200; // answer at http://oeis.org/A084422/b084422.txt
numsetvec primeFactors(MAXCALC +1);

typedef std::vector<numtype> numvec;

// Caching / memoization
typedef std::map<numvec, double> numvec2dbl;
numvec2dbl set2NumCoPrimeSets;

double NumCoPrimeSets(const numvec& initialSet)
{
    // Preprocessing step: remove numbers which are already coprime
    typedef std::unordered_map<numtype, numvec> num2numvec;
    num2numvec prime2Elts;
    for(numtype num : initialSet) {
        const numset& factors = primeFactors[num];
        for(numtype factor : factors) {
             prime2Elts[factor].push_back(num);
        }
    }

    numset eltsToRemove(initialSet.begin(), initialSet.end());
    typedef std::vector<std::pair<numtype,int>> numintvec;
    numvec primesRemaining;
    for(const num2numvec::value_type& primeElts : prime2Elts) {
        if (primeElts.second.size() > 1) {
            for (numtype num : primeElts.second) {
                eltsToRemove.erase(num);
            }
            primesRemaining.push_back(primeElts.first);
        }
    }

    double mult = pow(2.0, eltsToRemove.size());
    if (eltsToRemove.size() == initialSet.size())
        return mult;

    // Do the removal by creating a new set
    numvec set;
    for(numtype num : initialSet) {
        if (eltsToRemove.find(num) == eltsToRemove.end()) {
            set.push_back(num);
        }
    }

    // Transform to use a smaller set of primes before checking the cache
    // (beta code but it seems to work, mostly!)
    std::sort(primesRemaining.begin(), primesRemaining.end());
    numvec::const_iterator p = primesRemaining.begin();
    for(int j=0; p!= primesRemaining.end() && j<NPRIMES; ++p, ++j) {
        const numtype primeRemaining = *p;
        if (primeRemaining != PRIMES[j]) {
            for(numtype& num : set) {
                while (num % primeRemaining == 0) {
                    num = num / primeRemaining * PRIMES[j];
                }
            }
        }
    }

    // Caching / memoization
    const numvec2dbl::const_iterator i = set2NumCoPrimeSets.find(set);
    if (i != set2NumCoPrimeSets.end())
        return mult * i->second;

    // Remove the most connected number
    typedef std::unordered_map<numtype, int> num2int;
    num2int num2ConnectionCount;
    for(numvec::const_iterator srcIt=set.begin(); srcIt!=set.end(); ++srcIt) {
        const numtype src = *srcIt;
        const numset& srcFactors = primeFactors[src];
        for(numvec::const_iterator tgtIt=srcIt +1; tgtIt!=set.end(); ++tgtIt) {
            for(numtype factor : srcFactors) {
                const numtype tgt = *tgtIt;
                if (tgt % factor == 0) {
                    num2ConnectionCount[src]++;
                    num2ConnectionCount[tgt]++;
                }
            }
        }
    }
    num2int::const_iterator connCountIt = num2ConnectionCount.begin();

    numtype numToErase = connCountIt->first;
    int maxConnCount = connCountIt->second;
    for (; connCountIt!=num2ConnectionCount.end(); ++connCountIt) {
        if (connCountIt->second > maxConnCount || connCountIt->second == maxConnCount && connCountIt->first > numToErase) {
            numToErase = connCountIt->first;
            maxConnCount = connCountIt->second;
        }
    }

    // Result is the number of coprime sets in:
    //      setA, the set that definitely has a chosen element of the input present
    // +    setB, the set the doesn't have the chosen element(s) of the input present

    // Because setA definitely has a chosen element, we remove elements it isn't coprime with
    // We also remove the chosen element(s): as they are definitely present it doesn't make any
    // difference to the number of sets
    numvec setA(set);
    const numset& factors = primeFactors[numToErase];
    for(numtype factor : factors) {
        setA.erase(std::remove_if(setA.begin(), setA.end(),
            [factor] (numtype i) { return i % factor == 0; } ), setA.end());
    }

    // setB: remove all elements which have the same prime factors
    numvec setB(set);
    setB.erase(std::remove_if(setB.begin(), setB.end(),
        [&factors] (numtype i) { return primeFactors[i] == factors; }), setB.end());
    const size_t numEltsWithSamePrimeFactors = (set.size() - setB.size());

    const double numCoPrimeSets = 
        numEltsWithSamePrimeFactors * NumCoPrimeSets(setA) + NumCoPrimeSets(setB);

    // Caching / memoization
    set2NumCoPrimeSets.insert(numvec2dbl::value_type(set, numCoPrimeSets));
    return mult * numCoPrimeSets;
}

int main(int argc, char* argv[])
{
    // Calculate prime numbers that factor into each number upto MAXCALC
    for(numtype i=2; i<=MAXCALC; ++i) {
        for(numtype j=0; j<NPRIMES; ++j) {
            if (i % PRIMES[j] == 0) {
                primeFactors[i].insert(PRIMES[j]);
            }
        }
    }

    const clock_t start = clock();

    std::ofstream fout("out.txt");

    for(numtype n=0; n<=MAXCALC; ++n) {
        numvec v;
        for(numtype i=1; i<=n; ++i) {
            v.push_back(i);
        }
        const clock_t now = clock();
        const clock_t ms = now - start;
        const double numCoPrimeSubsets = NumCoPrimeSets(v);
        fout << n << ", " << std::fixed << numCoPrimeSubsets << ", " << ms << "\n";
        std::cout << n << ", " << std::fixed << numCoPrimeSubsets << ", " << ms << "\n";
    }

    return 0;
}

It's possible to process upto n=600 in about 5 minutes. Time still looks exponential however, doubling every 50 to 60 n or so. The graph for calculating just one n is shown below.

---

Edit 2

This solution is much more naturally implemented in terms of a graph. Two more optimizations arose:

• Most importantly, if the graph G can be partitioned into two sets A and B such that there are no connections between A and B, then coprimes(G) = coprimes(A) * coprimes(B).

• Secondly, it's possible to collapse all numbers for a set of prime factors into a single node, so the value for the node is the count of numbers for its prime factors.

In the code below the Graph class holds the original adjacency matrix and the node values, and the FilteredGraph class holds the current list of remaining nodes as a bitset so that as nodes are removed, the new adjacency matrix can be calculated by bit masking (and there is relatively little data to pass in the recursion).

#include "Primes.h"

#include <cassert>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <ctime>

// Graph declaration

const int MAXGROUPS = 1462; // empirically determined

class Graph
{
    typedef std::bitset<MAXGROUPS> bitset;
    typedef std::vector<bitset> adjmatrix;
    typedef std::vector<int> intvec;
public:
    Graph(int numNodes)
        : m_nodeValues(numNodes), m_adjMatrix(numNodes) {}
    void SetNodeValue(int i, int v) { m_nodeValues[i] = v; }
    void SetConnection(int i, int j)
    {
        m_adjMatrix[i][j] = true;
        m_adjMatrix[j][i] = true;
    }
    int size() const { return m_nodeValues.size(); }
private:
    adjmatrix m_adjMatrix;
    intvec m_nodeValues;
    friend class FilteredGraph;
};

class FilteredGraph
{
    typedef Graph::bitset bitset;
public:
    FilteredGraph(const Graph* unfiltered);

    int FirstNode() const;
    int RemoveNode(int node);
    void RemoveNodesConnectedTo(int node);

    double RemoveDisconnectedNodes();

    bool AttemptPartition(FilteredGraph* FilteredGraph);

    size_t Hash() const { return std::hash<bitset>()(m_includedNodes); }
    bool operator==(const FilteredGraph& x) const
    { return x.m_includedNodes == m_includedNodes && x.m_unfiltered == m_unfiltered; }

private:
    bitset RawAdjRow(int i) const {
        return m_unfiltered->m_adjMatrix[i];
    }
    bitset AdjRow(int i) const {
        return RawAdjRow(i) & m_includedNodes;
    }
    int NodeValue(int i) const {
        return m_unfiltered->m_nodeValues[i];
    }

    const Graph* m_unfiltered;
    bitset m_includedNodes;
};

// Cache
namespace std {
    template<>
    class hash<FilteredGraph> {
    public:
        size_t operator()(const FilteredGraph & x) const { return x.Hash(); }
    };
}
typedef std::unordered_map<FilteredGraph, double> graph2double;
graph2double cache;

// MAIN FUNCTION

double NumCoPrimesSubSets(const FilteredGraph& graph)
{
    graph2double::const_iterator cacheIt = cache.find(graph);
    if (cacheIt != cache.end())
        return cacheIt->second;

    double rc = 1;

    FilteredGraph A(graph);
    FilteredGraph B(graph);

    if (A.AttemptPartition(&B)) {
        rc = NumCoPrimesSubSets(A);
        A = B;
    }

    const int nodeToRemove = A.FirstNode();
    if (nodeToRemove < 0) // empty graph
        return 1;

    // Graph B is the graph with a node removed
    B.RemoveNode(nodeToRemove);

    // Graph A is the graph with the node present -- and hence connected nodes removed
    A.RemoveNodesConnectedTo(nodeToRemove);
    // The number of numbers in the node is the number of times it can be reused
    const double removedNodeValue = A.RemoveNode(nodeToRemove);

    const double A_disconnectedNodesMult = A.RemoveDisconnectedNodes();
    const double B_disconnectedNodesMult = B.RemoveDisconnectedNodes();

    const double A_coprimes = NumCoPrimesSubSets(A);
    const double B_coprimes = NumCoPrimesSubSets(B);

    rc *= removedNodeValue * A_disconnectedNodesMult * A_coprimes
                           + B_disconnectedNodesMult * B_coprimes;

    cache.insert(graph2double::value_type(graph, rc));
    return rc;
}

// Program entry point
int Sequence2Graph(Graph** ppGraph, int n);

int main(int argc, char* argv[])
{
    const clock_t start = clock();

    int n=800; // runs in approx 6s on my machine

    Graph* pGraph = nullptr;

    const int coPrimesRemoved = Sequence2Graph(&pGraph, n);
    const double coPrimesMultiplier = pow(2,coPrimesRemoved);
    const FilteredGraph filteredGraph(pGraph);
    const double numCoPrimeSubsets = coPrimesMultiplier * NumCoPrimesSubSets(filteredGraph);
    delete pGraph;
    cache.clear(); // as it stands the cache can't cope with other Graph objects, e.g. for other n

    const clock_t now = clock();
    const clock_t ms = now - start;
    std::cout << n << ", " << std::fixed << numCoPrimeSubsets << ", " << ms << "\n";

    return 0;
}

// Graph implementation

FilteredGraph::FilteredGraph(const Graph* unfiltered)
    : m_unfiltered(unfiltered)
{
    for(int i=0; i<m_unfiltered->size(); ++i) {
        m_includedNodes.set(i);
    }
}

int FilteredGraph::FirstNode() const
{
    int firstNode=0;
    for(; firstNode<m_unfiltered->size() && !m_includedNodes.test(firstNode); ++firstNode) {
    }
    if (firstNode == m_unfiltered->size())
        return -1;
    return firstNode;
}

int FilteredGraph::RemoveNode(int node)
{
    m_includedNodes.set(node, false);
    return NodeValue(node);
}

void FilteredGraph::RemoveNodesConnectedTo(const int node)
{
    const bitset notConnected = ~RawAdjRow(node);
    m_includedNodes &= notConnected;
}

double FilteredGraph::RemoveDisconnectedNodes()
{
    double mult = 1.0;
    for(int i=0; i<m_unfiltered->size(); ++i) {
        if (m_includedNodes.test(i)) {
            const int conn = AdjRow(i).count();
            if (conn == 0) {
                m_includedNodes.set(i, false);;
                mult *= (NodeValue(i) +1);
            }
        }
    }
    return mult;
}

bool FilteredGraph::AttemptPartition(FilteredGraph* pOther)
{
    typedef std::vector<int> intvec;
    intvec includedNodesCache;
    includedNodesCache.reserve(m_unfiltered->size());
    for(int i=0; i<m_unfiltered->size(); ++i) {
        if (m_includedNodes.test(i)) {
            includedNodesCache.push_back(i);
        }
    }

    if (includedNodesCache.empty())
        return false;

    const int startNode= includedNodesCache[0];

    bitset currFoundNodes;
    currFoundNodes.set(startNode);
    bitset foundNodes;
    do {
        foundNodes |= currFoundNodes;
        bitset newFoundNodes;
        for(int i : includedNodesCache) {
            if (currFoundNodes.test(i)) {
                newFoundNodes |= AdjRow(i);
            }
        }
        newFoundNodes &= ~ foundNodes;
        currFoundNodes = newFoundNodes;
    } while(currFoundNodes.count() > 0);

    const size_t foundCount = foundNodes.count();
    const size_t thisCount = m_includedNodes.count();

    const bool isConnected = foundCount == thisCount;

    if (!isConnected) {
        if (foundCount < thisCount) {
            pOther->m_includedNodes = foundNodes;
            m_includedNodes &= ~foundNodes;
        }
        else {
            pOther->m_includedNodes = m_includedNodes;
            pOther->m_includedNodes &= ~foundNodes;
            m_includedNodes = foundNodes;
        }
    }

    return !isConnected;
}


// Initialization code to convert sequence from 1 to n into graph
typedef short numtype;
typedef std::set<numtype> numset;

bool setIntersect(const numset& setA, const numset& setB)
{
    for(int a : setA) {
        if (setB.find(a) != setB.end())
            return true;
    }
    return false;
}

int Sequence2Graph(Graph** ppGraph, int n)
{
    typedef std::map<numset, int> numset2int;
    numset2int factors2count;

    int coPrimesRemoved = n>0; // for {1}
    // Calculate all sets of prime factors, and how many numbers belong to each set
    for(numtype i=2; i<=n; ++i) {
        if ((i > n/2) && (std::find(PRIMES, PRIMES+NPRIMES, i) !=PRIMES+NPRIMES)) {
            ++coPrimesRemoved;
        }
        else {
            numset factors;
            for(numtype j=0; j<NPRIMES && PRIMES[j]<n; ++j) {
                if (i % PRIMES[j] == 0) {
                    factors.insert(PRIMES[j]);
                }
            }
            factors2count[factors]++;
        }
    }

    // Create graph
    Graph*& pGraph = *ppGraph;
    pGraph = new Graph(factors2count.size());
    int srcNodeNum = 0;
    for(numset2int::const_iterator i = factors2count.begin(); i!=factors2count.end(); ++i) {
        pGraph->SetNodeValue(srcNodeNum, i->second);
        numset2int::const_iterator j = i;
        int tgtNodeNum = srcNodeNum+1;
        for(++j; j!=factors2count.end(); ++j) {
            if (setIntersect(i->first, j->first)) {
                pGraph->SetConnection(srcNodeNum, tgtNodeNum);
            }
            ++tgtNodeNum;
        }
        ++srcNodeNum;
    }

    return coPrimesRemoved;
}

The graph for calculating coprimes(n) is shown below in red (with the old approach in black).

Based on the (exponential) rate of increase observed, the prediction for n=3000 is 30 hours, assuming that the program doesn't blow up. This is starting to look computationally feasible, especially with more optimizations, but is nowhere near the 5s that is required! No doubt the required solution is short and sweet, but this has been fun...

Answer 3

Here's something rather straightforward in Haskell, which takes about 2 seconds for n=200 and slows exponentially.

{-# OPTIONS_GHC -O2 #-}   

f n = 2^(length second + 1) * (g [] first 0) where
  second = filter (\x -> isPrime x && x > div n 2) [2..n]
  first = filter (flip notElem second) [2..n]
  isPrime k = 
    null [ x | x <- [2..floor . sqrt . fromIntegral $ k], k `mod`x  == 0]
  g s rrs depth
    | null rrs = 2^(length s - depth)
    | not $ and (map ((==1) . gcd r) s) = g s rs depth 
                                        + g s' rs' (depth + 1)
    | otherwise = g (r:s) rs depth
   where r:rs = rrs
         s' = r : filter ((==1) . gcd r) s
         rs' = filter ((==1) . gcd r) rs

Answer 4

Here's an approach that gets the given sequence upto n=62 in under 5s (with optimizations it runs n=75 in 5s, however note my second attempt at this problem does better). I'm assuming the modulo part of the problem is just to do with avoiding numerical errors as the function gets large, so I'm ignoring it for now.

The approach is based on the fact that we can choose at most one number in a subset for each prime.

• We start with the first prime, 2. If we don't include 2, then we have 1 combination for this prime. If we do include 2, then we have as many combinations as they are numbers divisible by 2.
• Then we go onto the second prime, 3, and decide whether or not to include that. If we don't include it, we have 1 combination for this prime. If we do include 2, then we have as many combinations as they are numbers divisible by 3.
• ... and so on.

Taking the example {1,2,3,4}, we map the numbers in the set onto primes as follows. I've included 1 as a prime as it makes the exposition easier at this stage.

1 → {1}
2 → {2,4}
3 → {3}

We have 2 combinations for the "prime" 1 (don't include it or 1), 3 combinations for the prime 2 (don't include it or 2 or 4), and 2 combinations for 3 (don't include it or 3). So the number of subsets is 2 * 3 * 2 = 12.

Similarly for {1,2,3,4,5} we have

1 → {1}
2 → {2,4}
3 → {3}
5 → {5}

giving 2 * 3 * 2 * 2= 24.

But for {1,2,3,4,5,6}, things aren't so straightforward. We have

1 → {1}
2 → {2,4,6}
3 → {3}
5 → {5}

but if we choose the number 6 for the prime 2, we can't choose a number for the prime 3 (as a footnote, in my first approach, which I may come back to, I treated this as though the choices for 3 were cut in half when we chose 6, so I used 3.5 rather than 4 for the number of combinations for the prime 2 and 2 * 3.5 * 2 * 2 = 28 gave the right answer. I couldn't get this approach to work beyond n=17, however.)

The way I dealt with this is to split up the processing for each set of prime factors at each level. So {2,4} have prime factors {2}, whereas {6} has prime factors {2,3}. Omitting the spurious entry for 1 (which isn't a prime), we now have

2 → {{2}→{2,4}, {2,3}→6}
3 → {{3}→{3}}
5 → {{5}→{5}}

Now there are three paths to calculate the number of combinations, one path where we don't select the prime 2, and two paths where we do: through {2}→{2,4} and through {2,3}→6.

• The first path has 1 * 2 * 2 = 4 combinations because we can either select 3 or not, and we can either select 5 or not.
• Similarly the second has 2 * 2 * 2 = 8 combinations noting that we can choose either 2 or 4.
• The third has 1 * 1 * 2 = 2 combinations, because we only have one choice for the prime 3 -- not to use it.

In total this gives us 4 + 8 + 2 = 14 combinations (as an optimization note that the first and second paths could have been collapsed together to get 3 * 2 * 2 = 12). We also have the choice of selecting 1 or not, so the total number of combinations is 2 * 14 = 28.

C++ code to recursively run through the paths is below. (It's C++11, written on Visual Studio 2012, but ought to work on other gcc as I haven't included anything platform specific).

#include <cassert>
#include <vector>
#include <set>
#include <algorithm>
#include <iterator>
#include <iostream>
#include <ctime>

const int PRIMES[] = // http://rlrr.drum-corps.net/misc/primes1.shtml
    { 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
        53, 59, 61, 67, 71, 73, 79, 83, 89, 97,
        103, 107, 109, 113, 127, 131, 137, 139, 149,
        151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199 };
const int NPRIMES = sizeof(PRIMES) / sizeof(int);

typedef std::vector<int> intvec;
typedef std::set<int> intset;
typedef std::vector<std::set<int>> intsetvec;

struct FactorSetNumbers
{
    intset factorSet;
    intvec numbers; // we only need to store numbers.size(), but nice to see the vec itself
    FactorSetNumbers() {}
    FactorSetNumbers(const intset& factorSet_, int n)
        : factorSet(factorSet_)
    {
        numbers.push_back(n);
    }
};
typedef std::vector<FactorSetNumbers> factorset2numbers;
typedef std::vector<factorset2numbers> factorset2numbersArray;

double NumCoPrimeSubsets(
    const factorset2numbersArray& factorSet2Numbers4FirstPrime,
    int primeIndex, const intset& excludedPrimes)
{
    const factorset2numbers& factorSet2Numbers = factorSet2Numbers4FirstPrime[primeIndex];
    if (factorSet2Numbers.empty())
        return 1;

    // Firstly, we may choose not to use this prime number at all
    double numCoPrimeSubSets = NumCoPrimeSubsets(factorSet2Numbers4FirstPrime,
        primeIndex + 1, excludedPrimes);
    // Optimization: if we're not excluding anything, then we can collapse
    // the above call and the first call in the loop below together
    factorset2numbers::const_iterator i = factorSet2Numbers.begin();
    if (excludedPrimes.empty()) {
        const FactorSetNumbers& factorSetNumbers = *i;
        assert(factorSetNumbers.factorSet.size() == 1);
        numCoPrimeSubSets *= (1 + factorSetNumbers.numbers.size());
        ++i;
    }
    // We are using this prime number. The number of subsets for this prime number is the sum of
    // the number of subsets for each set of integers whose factors don't include an excluded factor
    for(; i!=factorSet2Numbers.end(); ++i) {
        const FactorSetNumbers& factorSetNumbers = *i;
        intset intersect;
        std::set_intersection(excludedPrimes.begin(),excludedPrimes.end(),
            factorSetNumbers.factorSet.begin(),factorSetNumbers.factorSet.end(),
            std::inserter(intersect,intersect.begin()));
        if (intersect.empty()) {
            intset unionExcludedPrimes;
            std::set_union(excludedPrimes.begin(),excludedPrimes.end(),
                factorSetNumbers.factorSet.begin(),factorSetNumbers.factorSet.end(),
                std::inserter(unionExcludedPrimes,unionExcludedPrimes.begin()));
            // Optimization: don't exclude on current first prime,
            // because can't possibly occur later on
            unionExcludedPrimes.erase(unionExcludedPrimes.begin());
            numCoPrimeSubSets += factorSetNumbers.numbers.size() *
                NumCoPrimeSubsets(factorSet2Numbers4FirstPrime,
                    primeIndex + 1, unionExcludedPrimes);
        }
    }
    return numCoPrimeSubSets;
}

int main(int argc, char* argv[])
{
    const int MAXCALC = 80;

    intsetvec primeFactors(MAXCALC +1);
    // Calculate prime numbers that factor into each number upto MAXCALC
    for(int i=2; i<=MAXCALC; ++i) {
        for(int j=0; j<NPRIMES; ++j) {
            if (i % PRIMES[j] == 0) {
                primeFactors[i].insert(PRIMES[j]);
            }
        }
    }

    const clock_t start = clock();

    factorset2numbersArray factorSet2Numbers4FirstPrime(NPRIMES);
    for(int n=2; n<=MAXCALC; ++n) {
        {
            // For each prime, store all the numbers whose first prime factor is that prime
            // E.g. for the prime 2, for n<=20, we store
            // {2},       { 2,  4,  8, 16 }
            // {2, 3},    { 6, 12, 18 }
            // {2, 5},    { 5, 10, 20 }
            // {2, 7},    { 14 }
            const int firstPrime = *primeFactors[n].begin();
            const int firstPrimeIndex = std::find(PRIMES, PRIMES + NPRIMES, firstPrime) - PRIMES;
            factorset2numbers& factorSet2Numbers = factorSet2Numbers4FirstPrime[firstPrimeIndex];
            const factorset2numbers::iterator findFactorSet = std::find_if(factorSet2Numbers.begin(), factorSet2Numbers.end(),
                [&](const FactorSetNumbers& x) { return x.factorSet == primeFactors[n]; });
            if (findFactorSet == factorSet2Numbers.end()) {
                factorSet2Numbers.push_back(FactorSetNumbers(primeFactors[n], n));
            }
            else {
                findFactorSet->numbers.push_back(n);
            }

            // The number of coprime subsets is the number of coprime subsets for the first prime number,
            // starting with an empty exclusion list
            const double numCoPrimeSubSetsForNEquals1 = 2;
            const double numCoPrimeSubsets = numCoPrimeSubSetsForNEquals1 *
                NumCoPrimeSubsets(factorSet2Numbers4FirstPrime,
                0, // primeIndex
                intset()); // excludedPrimes
            const clock_t now = clock();
            const clock_t ms = now - start;
            std::cout << n << ", " << std::fixed << numCoPrimeSubsets << ", " << ms << "\n";
        }
    }

    return 0;
}

Timings: computes the sequence upto 40 in <0.1s, the sequence upto 50 in 0.5s, to 60 in 2.5s, to 70 in 20s, and to 80 in 157s.

Although this certainly seems to output the right numbers it is, as might be expected, too costly. In particular it takes at least exponential time (and quite possibly combinatorial time).

Clearly this approach doesn't scale as required. However there may be something here which gives other people ideas (or rules out this approach as a failure). It seems like there are two possibilities:

1. This approach can be made to work, because of some combination of the following.
   • There are some clever mathematical optimizations I haven't spotted which eliminate calculations altogether.
   • There are some efficiency optimizations, e.g. use bitset rather than set.
   • Caching. This seems most promising, in that it might be possible to change the recursive call structure into a tree structure, which could be incrementally updated (where a parent-child relationship indicates multiply, and sibling relationship indicates add).
     
2. This approach can't be made to work.
   • There is some approach that is largely unrelated to this one.
   • It's possible that the first approach I used might be made to work. This was much more of a "closed form" solution that worked very efficiently for upto n=17 and failed at n=18 and above, being out by a small number. I spent a long time writing up the patterns and trying to figure out why it suddenly failed for n=18, but couldn't see it. I may come back to this, or I will include it as an alternative answer if anyone is interested.

Edit: I've made some optimizations using a few tricks try to avoid redoing existing calculations where possible and the code is about 10x faster. Sounds good, but it's only a constant improvement. What's really needed is some insight into this problem -- e.g. can we base #subsets(n+1) on #subsets(n)?

Answer 5

This is how I would do it:

1. Find the prime factors mod m of the numbers up to n
2. Create a queue q of sets, and add to it the empty set, and set counter to 1
3. While the queue is not empty, pop an element X from the queue
4. For all the numbers k from max(X) to n, check if the factors of the set intersect with the factors of the numer. If not, add to the queue X U k and increment counter by 1. Otherwise, go to the next k.
5. Return counter

Two important things must be pointed out:

• You don't need the factorization of the numbers up to n, but just their prime factors, that means, for 12 you just need 2 and 3. This way checking if 2 numbers are coprime becomes checking if the intersection of two sets is empty.
• You can keep track of the "set of factors" of each new set you create, this way you won't have to test every new number against every other number in the set, but just intersct his prime factors set against the one of the whole set.

Answer 6

Here is a way in O(n*2^p), where p is the number of primes under n. Not making use of the modulus.

class FailureCoprimeSubsetCounter{
    int[] primes;//list of primes under n
    PrimeSet[] primeSets;//all 2^primes.length

    //A set of primes under n. And a count which goes with it.
    class PrimeSet{
        BitSet id;//flag x is 1 iff prime[x] is a member of this PrimeSet
        long tally;//number of coprime sets that do not have a factor among these primes and do among all the other primes
        //that is, we count the number of coprime sets whose maximal coprime subset of primes[] is described by this object
        PrimeSet(int np){...}
    }

    int coprimeSubsets(int n){
        //... initialization ...
        for(int k=1; k<=n; k++){
            PrimeSet p = listToPrimeSet(PrimeFactorizer.factorize(k)); 
            for(int i=0; i<Math.pow(2,primes.length); i++){
            //if p AND primes[i] is empty
                //add primes[i].tally to PrimeSet[ p OR primes[i] ]   
            }       
        }
        //return sum of all the tallies
    }
}

But since this is a competition problem, there must be a quicker and dirtier solution. And being that this method needs exponential time and space and there are 430 primes under 3000, something more elegant too.

Answer 7

EDIT: A recursive approach added. Solves in 5 seconds upto n = 50.

#include <iostream>
#include <vector>
using namespace std;


int coPrime[3001][3001] = {0};
int n, m;

// function that checks whether a new integer is coprime with all
//elements in the set S.
bool areCoprime ( int p, vector<int>& v ) {

    for ( int i = 0; i < v.size(); i++ ) {
        if ( !coPrime[v[i]][p] )
            return false;
    }

    return true;
}

// implementation of Euclid's GCD between a and b
bool isCoprimeNumbers( int a, int b ) {
    for ( ; ; ) {

        if (!(a %= b)) return b == 1 ;
        if (!(b %= a)) return a == 1 ;

   }
}

int subsets( vector<int>& coprimeList, int index ) {

    int count = 0;
    for ( int i = index+1; i <= n; i++ ) {

        if ( areCoprime( i, coprimeList ) ) {

            count = ( count + 1 ) % m;
            vector<int> newVec( coprimeList );
            newVec.push_back( i );

            count = ( count + subsets( newVec, i ) ) % m;

        }

    }
    return count;
}

int main() {

    cin >> n >> m;

    int count = 1; // empty set
    count += n; // sets with 1 element each.

    // build coPrime matrix
    for ( int i = 1; i <= 3000; i++ )
        for ( int j = i+1; j <= 3000; j++ )
            if ( isCoprimeNumbers( i, j ) )
                coPrime[i][j] = 1;

    // find sets beginning with i
    for ( int i = 1; i <= n; i++ ) {

        vector<int> empty;
        empty.push_back( i );
        count = ( count + subsets( empty, i ) ) % m;

    }

    cout << count << endl;

    return 0;
}

A naive approach can be (for N = 3000):

Step1: Build Boolean matrix
1. Build a list of prime numbers from 2 to 1500.
2. For each number 1 to 3000, build a set of its prime factors.
3. Compare each pair of sets and get a boolean matrix[3000][3000] that states whether element i and j are mutually coprime (1) or not (0).

Step 2: Calculate the number of coprime sets of length k (k = 0 to 3000)
1. Initialize count = 1 (empty set). Now k = 1. Maintain a list of sets of length k.
2. Build 3000 sets containing only that particular element. (increment the count)
3. Scan each element from k to 3000 and see if a new set can be formed by adding it to any of the existing sets of length k. Note: some newly formed sets may or may not be identical. If you use set of sets, then only unique sets shall be stored.
4. Delete all sets that still have a length k.
5. Increment count by the current number of unique sets.
6. k = k + 1 and goto step 3.

Alternatively, you can maintain a list of products of each of the elements in a set and check whether the new element is coprime with the product. In that case, you do not need to store the Boolean matrix.

The complexity for the above algorithm seems somewhere between O(n^2) and O(n^3).

Full Code in C++: (improvement: condition added that element should be checked in a set only if it is > than the largest value in the set).

#include <iostream>
#include <vector>
#include <set>
using namespace std;


int coPrime[3001][3001] = {0};

// function that checks whether a new integer is coprime with all
//elements in the set S.
bool areCoprime ( int p, set<int> S ) {

    set<int>::iterator it_set;
    for ( it_set = S.begin(); it_set != S.end(); it_set++ ) {
        if ( !coPrime[p][*it_set] )
            return false;
    }

    return true;
}

// implementation of Euclid's GCD between a and b
bool isCoprimeNumbers( int a, int b ) {
    for ( ; ; ) {

        if (!(a %= b)) return b == 1 ;
        if (!(b %= a)) return a == 1 ;

   }
}

int main() {

    int n, m;
    cin >> n >> m;

    int count = 1; // empty set

    set< set<int> > setOfSets;
    set< set<int> >::iterator it_setOfSets;


    // build coPrime matrix
    for ( int i = 1; i <= 3000; i++ )
        for ( int j = 1; j <= 3000; j++ )
            if ( i != j && isCoprimeNumbers( i, j ) )
                coPrime[i][j] = 1;

    // build set of sets containing 1 element.
    for ( int i = 1; i <= n; i++ ) {

        set<int> newSet;
        newSet.insert( i );

        setOfSets.insert( newSet );
        count = (count + 1) % m;

    }

    // Make sets of length k
    for ( int k = 2; k <= n; k++ ) {

        // Scane each element from k to n
        set< set<int> > newSetOfSets;
        for ( int i = k; i <= n; i++ ) {

            //Scan each existing set.
            it_setOfSets = setOfSets.begin();
            for ( ; it_setOfSets != setOfSets.end(); it_setOfSets++ ) {

                if ( i > *(( *it_setOfSets ).rbegin()) && areCoprime( i, *it_setOfSets ) ) {

                    set<int> newSet( *it_setOfSets );
                    newSet.insert( i );

                    newSetOfSets.insert( newSet );

                }


            }

        }

        count = ( count + newSetOfSets.size() ) % m;

        setOfSets = newSetOfSets;

    }

    cout << count << endl;

    return 0;
}

The above code seems to give correct result but consumes a lot of time: Say M is large enough:

For N = 4, count = 12. (almost instantaneous)
For N = 20, count = 3232. (2-3 seconds)
For N = 25, count = 11168. (2-3 seconds)
For N = 30, count = 31232 (4 seconds)
For N = 40, count = 214272 (30 seconds)

Answer 8

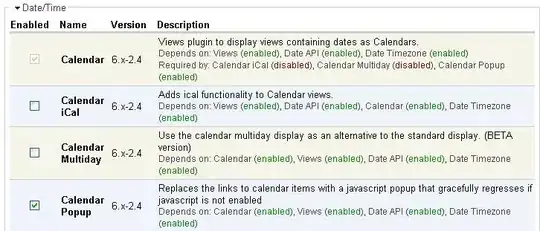
Here's the different approach I mentioned earlier.
It is indeed much faster than the one I used before. It can calculate up to coprime_subsets(117) in less than 5 seconds, using an online interpreter(ideone).

The code builds the possible sets starting from the empty set, and inserting every number into all possible subsets.

primes_to_3000 = set([2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287, 2293, 2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423, 2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617, 2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749, 2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909, 2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999])
# primes up to sqrt(3000), used for factoring numbers
primes = set([2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53])

factors = [set() for _ in xrange(3001)]
for p in primes:
    for n in xrange(p, 3001, p):
        factors[n].add(p)


def coprime_subsets(highest):
    count = 1
    used = {frozenset(): 1}
    for n in xrange(1, highest+1):
        if n in primes_to_3000:
            # insert the primes into all sets
            count <<= 1
            if n < 54:
                used.update({k.union({n}): v for k, v in used.iteritems()})
            else:
                for k in used:
                    used[k] *= 2
        else:
            for k in used:
                # only insert into subsets that don't share any prime factors
                if not factors[n].intersection(k):
                    count += used[k]
                    used[k.union(factors[n])] += used[k]
    return count

---

Here's my idea and an implementation in python. It seems to be slow, but I'm not sure if it's just the way I was testing(using an online interpreter)...
It could be that running it on a "real" computer might make a difference, but I can't test that at the moment.

There are two parts to this approach:

• Pre-generate a list of prime factors
• Create a cached recursive function for determining the number of possible subsets:
  • For each number, check its factors to see if it can be added to the subset
  • If it can be added, get the count for the recursive case, and add to total

After that, I guess you just take the modulo...

Here's my python implementation(improved version):

# primes up to 1500
primes = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499

factors = [set() for _ in xrange(3001)]
for p in primes:
    for n in xrange(p, 3001, p):
        factors[n].add(p)


def coprime_subsets(highest, current=1, factors_used=frozenset(), cache={}):
    """
    Determine the number of possible coprime subsets of numbers,
    using numbers starting at index current.
    factor_product is used for determining if a number can be added
    to the current subset.
    """
    if (current, factors_used) in cache:
        return cache[current, factors_used]
    count = 1
    for n in xrange(current, highest+1):
        if factors_used.intersection(factors[n]):
            continue
        count += coprime_subsets(highest, n+1, factors_used.union(factors[n]))
    cache[current, factors_used] = count
    return count

I also have another idea, which I will try implementing if I get the time. I believe a different approach might be quite a bit faster.

Answer 9

It looks like the proposed answers, as well as the preamble to the question, address a question different from the one asked.

The question was:

Output the number of coprime subsets of {1, 2, 3, ..., n} modulo m.

The proposed answers attempt to address another one:

Output the number of coprime subsets of {1, 2, 3, ..., n}.

These questions are NOT equivalent. The 1st one deals with the finite ring Z_m, and the 2nd one deals with the ring of integers Z which has completely different arithmetic.

Moreover, the definition "Two integers are coprime if their greatest common divisor equals 1" in the preamble to the question is not applicable to Z_m: finite rings don't have arithmetically stable comparison, so there's no such thing as a "greatest" common divisor.

The same objection applies to the example in the question: 3 and 4 are NOT relatively prime modulo 7 because both are divisible by 2 modulo 7: 4=(2*2)%7 and 3=(2*5)%7.

In fact, Z_m arithmetic is so weird that one can give the answer in O(1) time, at least for prime m: for any n and prime m there are NO coprime pairs modulo m. Here's why: Non-zero elements of Z_m form a cyclic group of order m-1, which implies that for any non-zero elements a and b from Z_m one can write a=bc for some c in Z_m. This proves that there are no coprime pairs in Z_m for prime m.

From the example in the question: let's take a look at {2, 3} mod 7 and {3, 4} mod 7: 2=(3*3)%7 and 3=(4*6)%7. Therefore {2,3} are not coprime in Z_7 (both are divisible by 3) and {3,4} are not coprime in Z_7 (both are divisible by 4).

Now let's consider the case of non-prime m. Write ma as a product of prime powers m=p_1^i_1*...*p_k^i_k. If a and b have a common prime factor than they are clearly not coprime. If at least one of them, say b, does not divide any of the primes p_1,...,p_k then a and b have a common factor for roughly the same reason as in the case of prime m: b would be a multiplicative unit of Z_m, and therefore a would be divisible by b in Z_m.

So it remains to consider the case when m is composite and a and b are divisible by distinct prime factors of m, let's say a is divisible by p and b is divisible by q. In this case they indeed can be coprimes. For example, 2 and 3 modulo 6 are coprimes.

So the question for coprime pairs boils down to these steps:

1. Finding prime factors of m that are less than n. If none then there are no coprime pairs.

2. Enumerating products of powers of these prime factors that remain the factors of m that are less than n.

3. Computing the number of Z-comprime pairs among thoses.