Is function 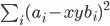 convex in x and y jointly? I want is to estimate both parameter x and y, that minimizes the least square. If the function is convex in both x and y jointly, then technically I can find x and y by iterating between 2 steps: Find best x given y and find best y given x.
convex in x and y jointly? I want is to estimate both parameter x and y, that minimizes the least square. If the function is convex in both x and y jointly, then technically I can find x and y by iterating between 2 steps: Find best x given y and find best y given x.
Obviously I know I might be wrong in multiple levels. Function look non-convex as there a multiple saddle point ie. all x=0 and y=0. But if I have a constrain that y>0, this problem is no longer there. Further, I am not sure whether the iterative algorithm work and converge even if the function is convex.