-5

What is the number of anagrams which are palindromes in a string? Example : string = "aaabbbb"; Possible anagram's which are palindromes "abbabba" , "bbaaabb" and "bababab". The problem here is the time, i have string of size 10^9. here's my final code can anybody tell me what's the wrong with it ?

Ahmed Mohsen
  • 73
  • 1
  • 9
  • Uhm, three? Seriously, you need to explain a little more "what you have done, and what you are struggling with". – Mats Petersson Jul 05 '13 at 23:37
  • ok, giving a string what's the number of permutation that's palindrome ? – Ahmed Mohsen Jul 05 '13 at 23:42
  • Show us what you've done, and tell us what problems you've run into. We want to see some code. – Borgleader Jul 05 '13 at 23:46
  • Here's the code :#include #include #include using namespace std; bool is_palindrome (string s){ string ss = s; reverse(ss.begin(),ss.end()); return(ss == s); } int main() { string s = "aaabbbb"; long long res = 0; sort(s.begin(),s.end()); do{ if(is_palindrome(s)){ cout << s < – Ahmed Mohsen Jul 05 '13 at 23:54
  • Sorry, this is better calculation: 7!/(3!*4!)=5040/144=35 is number of words. Check every of 35 words is it palindrome! – MrD Jul 05 '13 at 23:56

2 Answers2

9

Every letter in your input string has to appear in an even amount, execpt one letter can appear in an odd amount. This letter has a fixed position in the palindron. It has to be exactly in the middle. Lets say the amounts of the letter a,b,c,... are #a, #b, #c, ...

You only care about half of those letters, because in an palindron, the second half depands of the first half. So we only use half of the letters:

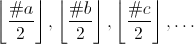
enter image description here

I used the floor function, so I calculate the letter, which appears in an odd amount, correct.

So how many permutations are in the first half? This is a case of distinct permutation, so we get

enter image description here

possibilities.

For your example: string = "aaabbbb";

We get: #a=3, #b=4. Therefore

enter image description here

We get 3 palindroms, these are "abbabba" , "bbaaabb" and "bababab", like you posted.

So, if you have a very large string:

  1. Count the amounts of each letter
  2. Check, if there is only 1 letter that appears in an odd amount. It there are more, you can't create palindroms.
  3. Use the formular to calculate the number of different palindroms.
Jakube
  • 3,353
  • 3
  • 23
  • 40
  • Thank you :) I think i get it :)) – Ahmed Mohsen Jul 06 '13 at 01:21
  • i think i have another problem that's if the string not sorting so i will not get all permutation "like your algorithm" ? – Ahmed Mohsen Jul 06 '13 at 02:03
  • That's no problem, just write a good counting function. I suggest: iterate through your input string and save the letters, which have appeared already. You can do this, by having two arrays, one, which contains the letters (a char array), and one, which contains the amount of this letter (int array). If a new letter appears, just add the letter in the first one and a 1 in the second one, if a already known letter appears, just increase the amount in the int array. – Jakube Jul 06 '13 at 08:10
0

Since each side of the anagram must be a mirror image of the other, the number of anagrams we care about is basically just the number of anagrams we can form on one side, so:

  1. group the characters in the string so identical characters are together (e.g., by sorting).
  2. Check for an odd number of more than one character (of so, # anagrams = 0).
  3. Take half the characters of each group of identical (truncating in the case of odd number).
  4. Compute the number of unique permutations of those characters.
Jerry Coffin
  • 476,176
  • 80
  • 629
  • 1,111
  • The problem here is the time to compute the number of unique permutations of those characters, the max size of string is 10^5 and what if the max size was 10^9 ? – Ahmed Mohsen Jul 06 '13 at 00:03
  • "The problem here is the time to compute the number of unique permutations" Calculating number of unique permutations is not problem, harder problem is to generate all permutations :) – MrD Jul 06 '13 at 00:07
  • Yup :) How i can solve this problem ? – Ahmed Mohsen Jul 06 '13 at 00:09
  • Given N items with M identical, the number of unique permutations is N! / M!. – Jerry Coffin Jul 06 '13 at 00:17
  • ok,right now i know the number of unique permutations how i can get the number of palindromes of this unique permutations ? – Ahmed Mohsen Jul 06 '13 at 00:23
  • @Ahmed_Mohsen: The number of unique permutations and number of palindromes is the same (assuming you divided each group by 2, as in the answer above). – Jerry Coffin Jul 06 '13 at 00:50
  • string s = "aaabbbb" the answer is 3. but using your algorithm the answer will be 7! / 2! = 1260 / 2 = 630 .. – Ahmed Mohsen Jul 06 '13 at 01:14
  • 1
    @Ahmed_Mohsen: You seem to have skipped step 3. – Jerry Coffin Jul 06 '13 at 01:40
  • I think i have another problem that's if the string not sorting so i will not get all permutation ? – Ahmed Mohsen Jul 06 '13 at 02:04
  • As noted, sorting is just a way of getting grouping. If it's (for example) too large to sort conveniently, you can (for example) count items instead (total number and number of each unique item). – Jerry Coffin Jul 06 '13 at 02:06
  • No,that's not the problem, string like this "ddaa" it's permutation is 0; bcuze it's not sorting so the answer will be zero , my code get 2 ? – Ahmed Mohsen Jul 06 '13 at 02:10