Projective transformation

Question

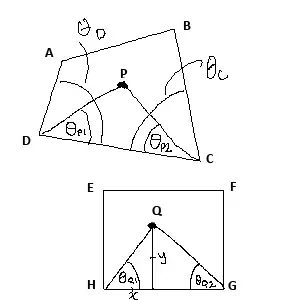
Given two image buffers (assume it's an array of ints of size width * height, with each element a color value), how can I map an area defined by a quadrilateral from one image buffer into the other (always square) image buffer? I'm led to understand this is called "projective transformation".

I'm also looking for a general (not language- or library-specific) way of doing this, such that it could be reasonably applied in any language without relying on "magic function X that does all the work for me".

An example: I've written a short program in Java using the Processing library (processing.org) that captures video from a camera. During an initial "calibrating" step, the captured video is output directly into a window. The user then clicks on four points to define an area of the video that will be transformed, then mapped into the square window during subsequent operation of the program. If the user were to click on the four points defining the corners of a door visible at an angle in the camera's output, then this transformation would cause the subsequent video to map the transformed image of the door to the entire area of the window, albeit somewhat distorted.

Answer 1

Using linear algebra is much easier than all that geometry! Plus you won't need to use sine, cosine, etc, so you can store each number as a rational fraction and get the exact numerical result if you need it.

What you want is a mapping from your old (x,y) co-ordinates to your new (x',y') co-ordinates. You can do it with matrices. You need to find the 2-by-4 projection matrix P such that P times the old coordinates equals the new co-ordinates. We'll assume that you're mapping lines to lines (not, for instance, straight lines to parabolas). Because you have a projection (parallel lines don't stay parallel) and translation (sliding), you need a factor of (xy) and (1), too. Drawn as matrices:

          [x  ]
[a b c d]*[y  ] = [x']
[e f g h] [x*y]   [y']
          [1  ]

You need to know a through h so solve these equations:

a*x_0 + b*y_0 + c*x_0*y_0 + d = i_0
a*x_1 + b*y_1 + c*x_1*y_1 + d = i_1
a*x_2 + b*y_2 + c*x_2*y_2 + d = i_2
a*x_3 + b*y_3 + c*x_3*y_3 + d = i_3

e*x_0 + f*y_0 + g*x_0*y_0 + h = j_0
e*x_1 + f*y_1 + g*x_1*y_1 + h = j_1
e*x_2 + f*y_2 + g*x_2*y_2 + h = j_2
e*x_3 + f*y_3 + g*x_3*y_3 + h = j_3

Again, you can use linear algebra:

[x_0 y_0 x_0*y_0 1]   [a e]   [i_0 j_0]
[x_1 y_1 x_1*y_1 1] * [b f] = [i_1 j_1]
[x_2 y_2 x_2*y_2 1]   [c g]   [i_2 j_2]
[x_3 y_3 x_3*y_3 1]   [d h]   [i_3 j_3]

Plug in your corners for x_n,y_n,i_n,j_n. (Corners work best because they are far apart to decrease the error if you're picking the points from, say, user-clicks.) Take the inverse of the 4x4 matrix and multiply it by the right side of the equation. The transpose of that matrix is P. You should be able to find functions to compute a matrix inverse and multiply online.

Where you'll probably have bugs:

• When computing, remember to check for division by zero. That's a sign that your matrix is not invertible. That might happen if you try to map one (x,y) co-ordinate to two different points.
• If you write your own matrix math, remember that matrices are usually specified row,column (vertical,horizontal) and screen graphics are x,y (horizontal,vertical). You're bound to get something wrong the first time.

Answer 2

EDIT

The assumption below of the invariance of angle ratios is incorrect. Projective transformations instead preserve cross-ratios and incidence. A solution then is:

1. Find the point C' at the intersection of the lines defined by the segments AD and CP.
2. Find the point B' at the intersection of the lines defined by the segments AD and BP.
3. Determine the cross-ratio of B'DAC', i.e. r = (BA' * DC') / (DA * B'C').
4. Construct the projected line F'HEG'. The cross-ratio of these points is equal to r, i.e. r = (F'E * HG') / (HE * F'G').
5. F'F and G'G will intersect at the projected point Q so equating the cross-ratios and knowing the length of the side of the square you can determine the position of Q with some arithmetic gymnastics.

---

Hmmmm....I'll take a stab at this one. This solution relies on the assumption that ratios of angles are preserved in the transformation. See the image for guidance (sorry for the poor image quality...it's REALLY late). The algorithm only provides the mapping of a point in the quadrilateral to a point in the square. You would still need to implement dealing with multiple quad points being mapped to the same square point.

Let ABCD be a quadrilateral where A is the top-left vertex, B is the top-right vertex, C is the bottom-right vertex and D is the bottom-left vertex. The pair (xA, yA) represent the x and y coordinates of the vertex A. We are mapping points in this quadrilateral to the square EFGH whose side has length equal to m.

Compute the lengths AD, CD, AC, BD and BC:

AD = sqrt((xA-xD)^2 + (yA-yD)^2)
CD = sqrt((xC-xD)^2 + (yC-yD)^2)
AC = sqrt((xA-xC)^2 + (yA-yC)^2)
BD = sqrt((xB-xD)^2 + (yB-yD)^2)
BC = sqrt((xB-xC)^2 + (yB-yC)^2)

Let thetaD be the angle at the vertex D and thetaC be the angle at the vertex C. Compute these angles using the cosine law:

thetaD = arccos((AD^2 + CD^2 - AC^2) / (2*AD*CD))
thetaC = arccos((BC^2 + CD^2 - BD^2) / (2*BC*CD))

We map each point P in the quadrilateral to a point Q in the square. For each point P in the quadrilateral, do the following:

• Find the distance DP:

  DP = sqrt((xP-xD)^2 + (yP-yD)^2)
  

• Find the distance CP:

  CP = sqrt((xP-xC)^2 + (yP-yC)^2)
  

• Find the angle thetaP1 between CD and DP:

  thetaP1 = arccos((DP^2 + CD^2 - CP^2) / (2*DP*CD))
  

• Find the angle thetaP2 between CD and CP:

  thetaP2 = arccos((CP^2 + CD^2 - DP^2) / (2*CP*CD))
  

• The ratio of thetaP1 to thetaD should be the ratio of thetaQ1 to 90. Therefore, calculate thetaQ1:

  thetaQ1 = thetaP1 * 90 / thetaD
  

• Similarly, calculate thetaQ2:

  thetaQ2 = thetaP2 * 90 / thetaC
  

• Find the distance HQ:

  HQ = m * sin(thetaQ2) / sin(180-thetaQ1-thetaQ2)
  

• Finally, the x and y position of Q relative to the bottom-left corner of EFGH is:

  x = HQ * cos(thetaQ1)
  y = HQ * sin(thetaQ1)
  

You would have to keep track of how many colour values get mapped to each point in the square so that you can calculate an average colour for each of those points.

Answer 3

I think what you're after is a planar homography, have a look at these lecture notes:

http://www.cs.utoronto.ca/~strider/vis-notes/tutHomography04.pdf

If you scroll down to the end you'll see an example of just what you're describing. I expect there's a function in the Intel OpenCV library which will do just this.

Answer 4

There is a C++ project on CodeProject that includes source for projective transformations of bitmaps. The maths are on Wikipedia here. Note that so far as i know, a projective transformation will not map any arbitrary quadrilateral onto another, but will do so for triangles, you may also want to look up skewing transforms.

Answer 5

If this transformation has to look good (as opposed to the way a bitmap looks if you resize it in Paint), you can't just create a formula that maps destination pixels to source pixels. Values in the destination buffer have to be based on a complex averaging of nearby source pixels or else the results will be highly pixelated.

So unless you want to get into some complex coding, use someone else's magic function, as smacl and Ian have suggested.

Answer 6

Here's how would do it in principle:

• map the origin of A to the origin of B via a traslation vector t.
• take unit vectors of A (1,0) and (0,1) and calculate how they would be mapped onto the unit vectors of B.
• this gives you a transformation matrix M so that every vector a in A maps to M a + t
• invert the matrix and negate the traslation vector so for every vector b in B you have the inverse mapping b -> M^-1 (b - t)
• once you have this transformation, for each point in the target area in B, find the corresponding in A and copy.

The advantage of this mapping is that you only calculate the points you need, i.e. you loop on the target points, not the source points. It was a widely used technique in the "demo coding" scene a few years back.