6

as we know tree structure could be represented in S-expressions. For example

 (5 (4 (11 (7 () ()) (2 () ()) ) ()) (8 (13 () ()) (4 () (1 () ()) ) ) )

But is it possible to use S-expression for a graph (esp. DAG)? e.g.

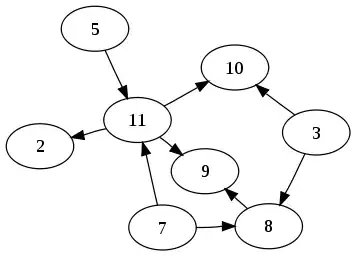
My second question is what is topology limit of S-expression can represent?

I Googled this quesion and couldn't find a clue, without a formal CS background, I am having trouble figuring this out myself. Please don't close this question. Thanks in advance!

Community
  • 1
  • 1
est
  • 11,429
  • 14
  • 70
  • 118

1 Answers1

6

Not as a recursive structure, like your binary tree.

  • You could use a list of nodes, and for each store which nodes it is has an edge to.

    ( (2 ())
  (3 (8 10))
  (5 (11))
  (7 (8 11))
  (8 (9))
  (9 ())
  (10 ())
  (11 (2 9 10)) )

  • You could store a list of nodes and edges.

    ( (2 3 5 7 8 9 10 11)
  ( (3 8)
    (3 10)
    (5 11)
    (7 8)
    (7 11)
    (8 9)
    (11 2)
    (11 9)
    (11 10) ) )
Markus Jarderot
  • 86,735
  • 21
  • 136
  • 138
  • that's cool, thanks. I Googled some spanning tree solution, still trying to figur it out – est Jun 05 '13 at 03:08
  • 1
    A spanning tree doesn't make much sense for a directed graph. You'd need at least one for every source-node (3, 5, 7). – Markus Jarderot Jun 05 '13 at 06:38