In python, with matplotlib, I have to draw 2 CDF curves on the same plot: one for data A, one for data B.
If I were to decide the "binning" myself, I would do the following and take 100 histograms based on data A. (in my case, A is always at most 50% of the size of B)
import numpy as np
import matplotlib
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.grid(True)
a = 0
nhist = 100
b = np.max(samplesFromA)
c = b-a
d = float(c) / float(nhist) #size of each bin
# tmp will contain a list of bins: [a, a+d, a+2*d, a+3*d, ... b]
tmp = [a]
for i in range(nhist):
if i == a:
continue
else:
tmp.append(tmp[i-1] + d)
# CDF of A
ax.hist(samplesFromA, bins=tmp, cumulative=True, normed=True,
color='red', histtype='step', linewidth=2.0,
label='samples A')
# CDF of B
plt.hist(samplesFromB, bins=tmp, cumulative=True, normed=True,
color='blue', alpha=0.5, histtype='step', linewidth=1.0,
label='samples B')
Here is the result (I cropped out all the non-relevant information):

Recently I've found out about sm.distributions.ECDF, which I wanted to compare to my previous implementation. Basically, I will just call the following function on my data (and decide elsewhere the the range of the rightmost bin), without computing any bins:
def drawCDF(ax, aSample):
ecdf = sm.distributions.ECDF(aSample)
x = np.linspace(min(aSample), max(aSample))
y = ecdf(x)
ax.step(x, y)
return ax
Here is the result, with the same data (again, I manually cropped out non-relevant text):
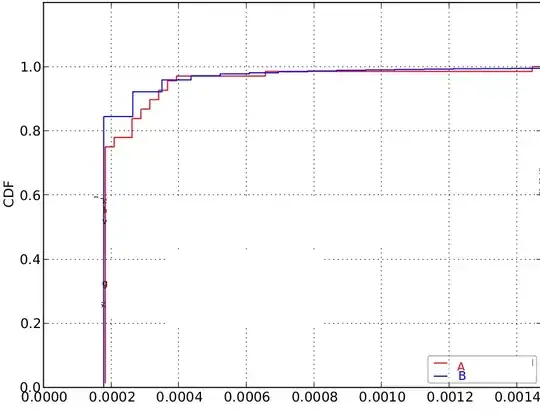
It turns out that this last example merges too many bins together and the result isn't a very well fine-grained CDF curve. What exactly happens behind the scenes here?
Sample A (in red) contains 70 samples, while sample B (in blue) contains 15 000!