I'm conducting a molecular dynamics simulation for silica. Some time ago I turned to the fluctuating dipole model, and after much effort I'm still having problems implementing it.
In short, all oxygen atoms in the system are polarizable, and their dipole moments depend on their position with respect to all the other atoms in the system. More particularly, I use TS potential (http://digitallibrary.sissa.it/bitstream/handle/1963/2874/tangney.pdf?sequence=2), where dipoles are found iteratively at each time step.
This means that when evaluating forces acting on atoms, I have to take into account this potential energy dependency on coordinates. Before, I was using simple pairwise potential models, and so I would set my program to compute forces using analytic formulas obtained by differentiating potential energy expression.
Now I'm at a loss: how to implement this new potential? In all the articles that I've found they only give you formulas, but not the algorithm. As I see it, when I compute forces, acting on a certain atom, I have to take into account the change of the dipole of this atom, the change of dipoles of all the neighboring atoms, then tge change of dipoles of still more atoms, and so on, as they depend on each other. After all, it is because of this interdependency that the dipoles are found iteratively at each time step. Clearly, I can't compute forces iteratively for each atom, because the computational complexity of the algorithm would be way too high. Should I use some simple functions to account for the change of dipoles? This doesn't look like a good idea either, cause dipoles are calculated iteratively, with high precision, and then, where it actually matters (computing forces), we would use crude functions?
So how do I implement this model? Also, is it possible to compute forces analytically, as I did before, or is it necessary to compute them using finite difference formula for derivative?
I haven't found the answer for my question in literature, but if you know some article, or site, or book, where this material is highlighted, please, direct me to that source.
Thank you for your time!
==================================================================================
UPDATE:
Thank you for your answer. Unfortunately, this was not my question. I didn't ask how to compute dipoles, but how to compute forces given that those dipoles vary with movement considerably.
I tried to compute forces in straightforward manner (not taking into account dipoles interdependance via their distances, just compute the dipoles on each steps, then compute the forces as if those dipoles are static), but the results I got were not physically correct.
To analyze the situation, I set up a simulation of a system consisting of just two atoms: Si and O. They have opposite charges, and so they oscillate. And the energy time dependence graphic looks like this:
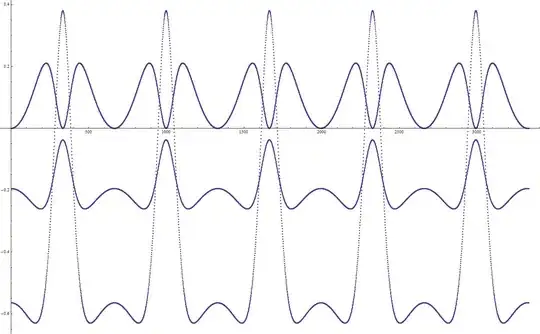
The curve on the top represents kinetic energy, the one in the middle represents potential energy without taking dipole interaction into account, and the one at the bottom represents potential energy of the system, where dipole interaction was taken into account.
You can clearly see from this graphic, that the system is doing what it shouldn't do: climbing up the potential slope. So I decided this is due to the fact that I didn't take dipole moment coordinate dependence into account. For instance, at a given time point, we compute the forces, and they are directed so as to move both atoms toward each other. But when we do move them towards each other (even slightly), the dipole moment changes, and we find out that we actually ended up with higher potential energy than before! During the next time step the situation is the same.
So the question is, how to take this effect into account, cause what few ways I can think of are either way too computationally intense, or way too crude.