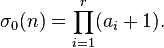How to divisor sieve numbers of form kn^p?

Question

Creating a divisor-counting sieve for all numbers 1-n is well known

func sieve(n)
    counts = array of size n+1, all elements set to 1, counts[0] = 0 arbitrary

    for 2 <= i <= n
        for i <= j <= n, stepwise i
            counts[j]++;
    return counts

However what if, instead of creating a sieve for numbers of form 1 * n, I wanted the divisor counts for numbers of form 6n^2 instead?

So instead of finding the divisor counts for 1, 2, 3, 4, 5, etc It might be instead looking for divisor counts of 6, 24, 54, 96, 150, etc

But really just numbers of form kn^p, in an efficient way so I am not actually storing an array of size kn^p at its largest. Seems like I should only need array of size N as before, only each spot represents the number of divisors of kn^p

Although a programming question in form, this seems really a mathematics question in substance. I think you will be better served at math.stackexchange.com, and have suggested that a moderator migrate it for you. — Pieter Geerkens, Apr 26 '13 at 03:07
@PieterGeerkens Except if I were to ask it there they would tell me to come here — RTG_FRE, Apr 26 '13 at 03:27
Wait a sec. What exactly are you asking about? I read the question 3 times and I dont get it. Are you asking how the maths will change, or how to generate the divisores, how to orchestrate the scan, or how to store the results, or something completely different..? — quetzalcoatl, Apr 26 '13 at 09:23
@quetzalcoatl: Count the number of divisors for all number of the form k*n^p, where k and p are fixed integer, and n are integers from 1. — nhahtdh, Apr 26 '13 at 17:48

score 3 · Accepted Answer · edited Feb 08 '17 at 14:41

Instead of counting the divisors directly, you can use this formula (taken from Wikipedia):

This will help you find the number of divisors for all square/cube/to the power of k numbers (n^k) while using O(n) memory.

// Stores the number of divisors for n^k
count[n + 1]

// Count number of divisors for 1^k, 2^k, ..., n^k
function countDivisors(n, k) {
    // Note: You can actually merge sieve function with the loop below
    prime[] = sieve(n)

    count[0] = 0
    count[1..n] = 1 // Set count[i] to count[n] to 1

    for all primes p <= n {
        for (i = 1; p^i <= n; i++) {
            // You can cache the value of p^i for next loop
            pi = p^i 

            for (m = pi; m <= n; m += pi) {
                // We "replace" the previous count with current count
                count[m] = count[m] / ((i - 1) * k + 1) * (i * k + 1)
            }
        }
    }
}

To extend it to a*n^k, find the prime factorization of a, and record the prime numbers along with the corresponding power.

If any prime is larger than n, you can take them away and reduce them to a multiplier according to the divisor function.

If any prime is smaller than n, supply it to the countDivisors function above, and modify the function a bit:

for all primes p <= n {
    // Note: You are free to optimize this in actual code
    let e be maximal power of p in a

    if (e > 0) {
        // Update all number with the factors from a
        for (i = 1; i <= n; i++) {
            count[i] *= (e + 1)
        }
    }

    for (i = 1; p^i <= n; i++) {
        // You can cache the value of p^i for next loop
        pi = p^i 

        for (m = pi; m <= n; m += pi) {
            // We "replace" the previous count with current count
            count[m] = count[m] / ((i - 1) * k + e + 1) * (i * k + e + 1)
        }
    }
}

As you can see, the time and space complexity does not depend on the power k, and only depends on n, the number of numbers whose number of divisors you want to find.

This unfortunately doesn't work when you start talking about integrating the a term — RTG_FRE, Apr 26 '13 at 17:43
@RTG_FRE: What make it fails to work? EDIT: Just fixed a typo. But if you got the idea from the n^p, then a*n^p should work similarly. — nhahtdh, Apr 26 '13 at 17:44
Even with the fix, not quite there yet. I more or less understand what you're going for though. hopefully I can figure out what's wrong — RTG_FRE, Apr 26 '13 at 17:47
@RTG_FRE: Let me check. I did implemented the n^p version, but haven't implemented k*n^p version. Do note that you need to take care of the case where a > max value that you loop to. (Will be back around 15 mins later) — nhahtdh, Apr 26 '13 at 17:49

How to divisor sieve numbers of form kn^p?

1 Answers1