k means clustering algorithm

Question

I want to perform a k means clustering analysis on a set of 10 data points that each have an array of 4 numeric values associated with them. I'm using the Pearson correlation coefficient as the distance metric. I did the first two steps of the k means clustering algorithm which were:

1) Select a set of initial centres of k clusters. [I selected two initial centres at random]

2) Assign each object to the cluster with the closest centre. [I used the Pearson correlation coefficient as the distance metric -- See below]

Now I need help understanding the 3rd step in the algorithm:

3) Compute the new centres of the clusters:

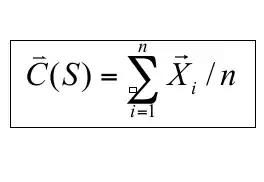
formula for new center condition

where X, in this case is a 4 dimensional vector and n is the number of data points in the cluster.

How would I go about calculating C(S) for say the following data?

# Cluster 1
A   10  15  20  25  # randomly chosen centre
B   21  33  21  23
C   43  14  23  23
D   37  45  43  49
E   40  43  32  32

# Cluster 2
F  100  102 143 212 #random chosen centre
G  303  213 212 302
H  102  329 203 212
I  32   201 430 48
J  60   99  87  34

The last step of the k means algorithm is to repeat step 2 and 3 until no object changes cluster which is simple enough.

I need help with step 3. Computing the new centres of the clusters. If someone could go through and explain how to compute the new centre of just one of the clusters, that would help me immensely.

why not post this quesiton here http://stats.stackexchange.com/ — gongzhitaao, Mar 24 '13 at 22:26
thanks for the link. I don't have enough reputation to post pictures in my questions there yet. Also I don't know how to typeset formulas into questions. — cooldood3490, Mar 24 '13 at 22:39

score 6 · Answer 1 · answered Mar 25 '13 at 08:41

Don't throw in other distance functions into k-means.

K-means is designed to minimize the "sum of squares", not distances! By minimizing the sum of squares, it will coincidentially minimize Squared Eudlidean and thus Euclidean distance, but this may not hold for other distances and thus K-means may stop converging when used with arbitrary distance functions.

Again: k-means does not minimize arbitrary distances. It minimizes the "sum of squares" which happens to agree with squared Euclidean distance.

If you want an algorithm that is well-defined for arbitrary distance functions, consider using k-medoids (Wikipedia), a k-means variant. PAM is guaranteed to converge with arbitrary distance functions.

mrueg · Accepted Answer · 2013-03-24T22:48:07.527

0

Step 3 corresponds to calculating the mean for each cluster. For cluster 1, you'd get as new cluster center (B+C+D+E) / 4, which is (35.25 33.75 29.75 21.75), i.e sum each component for all the points in the cluster separately, and divide it by the number of points in the cluster.

The cluster center (A for cluster 1) is usually not part of the calculation of the new cluster center.

edited Mar 24 '13 at 22:48

answered Mar 24 '13 at 22:27

mrueg

8,185
4
44
66

Okay I think I understand but isn't `(B+C+D+E) / 4` actually `(24.5 25.75 43.5 36.75)`? – cooldood3490 Mar 24 '13 at 22:37
That's not right (as was my original version, which is not corrected). e.g for the first component you'd have (21+43+37+40)/4 = 35.25 – mrueg Mar 24 '13 at 22:46
1

The second component of `(B+C+D+E) / 4` is `(33+14+45+43)/4`, i.e sum the take the second components of B,C,D,E and divide them by 4. – mrueg Mar 24 '13 at 22:54
You should include the previous centroid as part of the calculation of the new centroid. – stackoverflowuser2010 Mar 25 '13 at 17:51
1

If you are using *k centroids*, you certainly should. However, *k-means* is a similar, but not the same algorithm. – mrueg Mar 25 '13 at 22:01
1

@mrueg That is not correct. You are thinking of k-medoids. There is no k-centroid; it is the same as k-means. You are giving out bad information. – stackoverflowuser2010 Apr 05 '13 at 20:37
You're right. It's called k-medoids. My mistake. Still, k means does *not* include the previous centroid in the calculation of the new one. (The algorithm will basically still work, but convergence will probably to be somewhat slower.) – mrueg Apr 11 '13 at 00:37
@mrueg if the previous centroid is a data point (A), then it *is* included. – Has QUIT--Anony-Mousse Sep 09 '14 at 08:56

score 0 · Answer 3 · answered Mar 25 '13 at 00:03

For each cluster with n-dimensional points, calculate an n-dimensional center of mass to get the centroid. In your example, there are 4-dimensional points, so the center of mass is the mean along each of the 4 dimensions. For cluster 1, the centroid is: (30.20, 30.00, 27.80, 30.40). For example, the mean for the first dimension is calculated as (10+21+43+37+40)/5 = 30.20.

See the Wikipedia article on K-Means clustering for more information.

k means clustering algorithm

3 Answers3

Linked