I've managed to implement quadratic and cubic Bezier curves.They are pretty straightforward since we have a formula. Now I want to represent an n-th order Bezier curve using the generalization:
Where
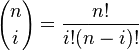
and
I'm using a bitmap library to render the output, so here is my code:
// binomialCoef(n, k) = (factorial(n) / (factorial(k) * factorial(n- k)))
unsigned int binomialCoef(unsigned int n, const unsigned int k)
{
unsigned int r = 1;
if(k > n)
return 0;
for(unsigned int d = 1; d <= k; d++)
{
r *= n--;
r /= d;
}
return r;
}
void nBezierCurve(Bitmap* obj, const Point* p, const unsigned int nbPoint, float steps, const unsigned char red, const unsigned char green, const unsigned char blue)
{
int bx1 = p[0].x;
int by1 = p[0].y;
int bx2;
int by2;
steps = 1 / steps;
for(float i = 0; i < 1; i += steps)
{
bx2 = by2 = 0;
for(int j = 0; (unsigned int)j < nbPoint; j++)
{
bx2 += (int)(binomialCoef(nbPoint, j) * pow(1 - i, (float)nbPoint - j) * pow(i, j) * p[j].x);
by2 += (int)(binomialCoef(nbPoint, j) * pow(1 - i, (float)nbPoint - j) * pow(i, j) * p[j].y);
}
bresenhamLine(obj, bx1, by1, bx2, by2, red, green, blue);
bx1 = bx2;
by1 = by2;
}
// curve must end on the last anchor point
bresenhamLine(obj, bx1, by1, p[nbPoint - 1].x, p[nbPoint - 1].y, red, green, blue);
}
Here's the set of points to render:
Point ncurv[] = {
20, 200,
70, 300,
200, 400,
250, 200
};
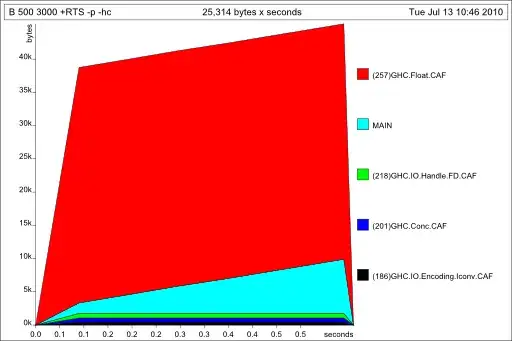
and here's the output:
The red curve is a cubic Bezier. The blue one is supposed to be the 4th order Bezier, which is the same as cubic Bezier, but in this case, they are not the same ?!
EDIT : I forgot to note that the bottom left point is (0, 0)