Mathematica - I want to approximate a root of this equation

Question

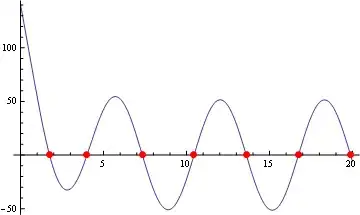
I have

f[x__]:=(Sqrt[2] Sqrt[-E^(-2 p x) g R (-2-14 p^2-E^(2 p x) Cos[x]+
         2 E^(2 p x) p^2 Cos[x]+3 E^(2 p x) p Sin[x])])/Sqrt[1+4 p^2]


g = 10
R = 2
p = 0.3

And I want to find a root for:

f[x]^2 == - g R Cos[x]

When I try Solve, I get: "This function cannot be solved with the methods available for Solve", the same for Reduce, and when I try Root: "... is not an univarirate polynomial"

How can I approximate a root of the equation above?

Answer 1

Plot[f[x]^2 + g R Cos[x], {x, 0, 20}, 
 Epilog -> {PointSize[Large], Red, Point[{x, 0} /. 
           Table[FindRoot[f[x]^2 + g R Cos[x] == 0, {x, i}], {i, 2, 20, 3}]]}]