Support vector machines - separating hyperplane question

Question

From what I've seen, seems like the separation hyperplane must be in the form

x.w + b = 0.

I don't get very well this notation. From what I understand, x.w is a inner product, so it's result will be a scalar. How can be it that you can represent a hyperplane by a scalar + b? I'm quite confused with this.

Also, even if it was x + b = 0, wouldn't it be of a hyperplane that passes right through the origin? From what I understand a separating hyperplane doesn't always pass through the origin!

remember that here **x** is the *"variable"*, i.e the plane is the set of all points **x** (x is a vector) that satisfy the equation w.x+b=0 — Amro, Oct 07 '09 at 10:30

score 17 · Accepted Answer · edited Apr 29 '19 at 10:04

17

It is the equation of a (hyper)plane using a point and normal vector.
Think of the plane as the set of points P such that the vector passing from P0 to P is perpendicular to the normal

Check out these pages for explanation:

http://mathworld.wolfram.com/Plane.html
http://en.wikipedia.org/wiki/Plane_%28geometry%29#Definition_with_a_point_and_a_normal_vector

edited Apr 29 '19 at 10:04

Glorfindel

21,988
13
81
109

answered Oct 07 '09 at 10:23

Amro

123,847
25
243
454

score 7 · Answer 2 · answered Oct 07 '09 at 10:05

7

Imagine a plane in a 3d coordinate system. To describe it, you need a normal vector N of that plane and the distance D of the plane to the origin. For simplicity, assume the normal vector has unit length. Then the equation for that plane is x.N - D = 0.

Explanation: x.N can be visualized as a projection of x on the normal vector N. The result is the length of vector x parallel to N. If this length equals D, the point x is on the plane.

answered Oct 07 '09 at 10:05

Niki

15,662
5
48
74

When you mean the distance of the plane to the origin, you mean the distance of the nearest point of the plane to the origin? – devoured elysium Oct 07 '09 at 10:14

score 6 · Answer 3 · answered Nov 23 '12 at 08:48

A definition of dot product (wich is an inner product) is

x . y = |x| * |y| * cos(a)

Where a is the smallest angle between x and y.

It is easy to see that x . y = 0, if a=90 deg (pi rad).

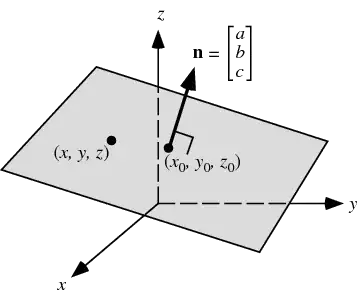
This means that if you have a fixed normal vector w, a hyperplane given by:

x . w = 0

is the set of all points that x can "point at" given that x has to be orthogonal to w.

Now, a hyperplane given by:

x . w + b = 0

is the set of all points that x can "point at" such that x . w is a constant. As x gets longer, |x| increases, the angle, a, has to get closer to 90 deg (pi rad), cos(a) decreases, to produce the same constant result. If you however take x pointing in the exact opposite direction of w, cos(a) = -1 and |x| = b (provided that w is of unit length).

It turns out that the plane given of this set of points is parallell to x . w = 0, and shifted in space the distance -b (in the direction of w) still given that w is of unit length.

This answer is probably not going to help the op, but hopefully someone else will benefit from it.

Support vector machines - separating hyperplane question

3 Answers3