I've used fitdistr function from R MASS package to adjust a Weibull 2 parameters probability density function (pdf).
This is my code:
require(MASS)
h = c(31.194, 31.424, 31.253, 25.349, 24.535, 25.562, 29.486, 25.680, 26.079, 30.556, 30.552, 30.412, 29.344, 26.072, 28.777, 30.204, 29.677, 29.853, 29.718, 27.860, 28.919, 30.226, 25.937, 30.594, 30.614, 29.106, 15.208, 30.993, 32.075, 31.097, 32.073, 29.600, 29.031, 31.033, 30.412, 30.839, 31.121, 24.802, 29.181, 30.136, 25.464, 28.302, 26.018, 26.263, 25.603, 30.857, 25.693, 31.504, 30.378, 31.403, 28.684, 30.655, 5.933, 31.099, 29.417, 29.444, 19.785, 29.416, 5.682, 28.707, 28.450, 28.961, 26.694, 26.625, 30.568, 28.910, 25.170, 25.816, 25.820)
weib = fitdistr(na.omit(h),densfun=dweibull,start=list(scale=1,shape=5))
hist(h, prob=TRUE, main = "", xlab = "x", ylab = "y", xlim = c(0,40), breaks = seq(0,40,5))
curve(dweibull(x, scale=weib$estimate[1], shape=weib$estimate[2]),from=0, to=40, add=TRUE)
Now, I would like to create the Weibull cumulative distribution function (cdf) and plot it as a graph:
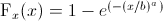 , where x > 0, b = scale , a = shape
, where x > 0, b = scale , a = shape
I tried to apply scale and shape parameters for h using the formula above, but it was not this way.