Last couple of days I spent on searching for curve reconstruction implementations, and found none - not as a library nor as a tool.
To describe my problem.
My main concern are contours with gaps:
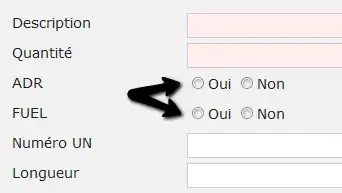
From papers I've read in the meantime, I guess solution will require usage of Delaunay triangulation, and the method referenced most seems to be described in 1997 paper "The Crust and the β-Skeleton: Combinatorial Curve Reconstruction "
Can someone point me to a curve reconstruction implementation, that can help me solve this problem?