Background
A list of integer coefficients can be used to represent a polynomial (in X). For example, 1 + 3x + 3x^2 + 2x^3 is represented by [1,3,3,2].
Let P be one of these lists.
I need to write axioms that take these coefficients and do different things with them.
Example: axioms for a relation eval(P,A,R) where R is the result of evaluating the polynomial represented by P at X = A (expect P and A to be fully instantiated). For example, eval([3,1,2],3,R) produces R=24. (This is because 3(3)^0 + 1(3)^1 + 2(3)^2 = 3 + 3 + 18 = 24).
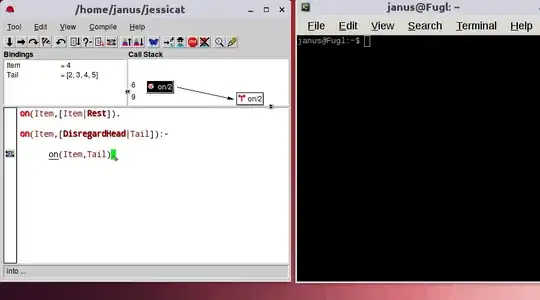
This Prolog tutorial discusses searching a list recursively: "It sees if something is the first item in the list. If it is, we succeed. If it is not, then we throw away the first item in the list and look at the rest".
on(Item,[Item|Rest]).
on(Item,[DisregardHead|Tail]):-
on(Item,Tail).
Question
How does this code throw away the first item in the list?
The question then becomes, once I've found it, how do I use it to calculate as described above?