I don't know how to write in Prolog but the grounded semantics are computed starting from arguments that weren't attacked, given the argument tree.
(Hope it guides @gusbro to find a proper answer to this thread.)
To explain how it's computed, I'll introduce the following function F(x) = {x defends y}, where:
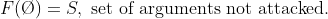
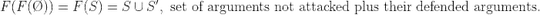
- If one defended argument is attacked by other deffended argument, then the attacked argument will be removed from the set.
- And so on, until the function cannot be more extended with more arguments, which it reached the minimal fix point in F.
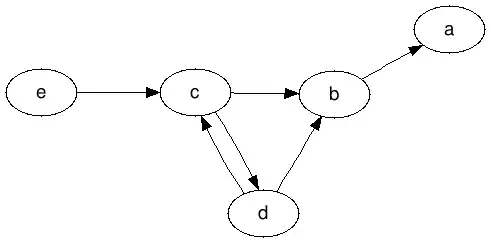
(Exemple 1) given the following argumentation graph, the grounded extension is Eg = {c, e, f, a}.

So, the first function begins with:
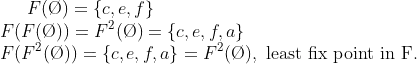
Now let consider computing of grounded extension with cycles.
(Example 2) In the given argumentation graph bellow, e defends b and d, but b is attacked by d, then it can't be included in the grounded semantics. From this point we have a conflict-free set {e, d}. From {e, d} we can apply agin the function F({e, d}) = {e, d, a}, where d defends a from b. Applying again the function F({e, d, a}) = {e, d, a}, showing that {e, d, a} is the minimal fix point in F. Therefore, {e, d, a} is the grounded extension.
(Example 3) In the argumentation tree below, the grounded extension 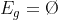 , since There aren't arguments that weren't attacked. Otherwise, If the argument e did not attack itself, the grounded extension should be
, since There aren't arguments that weren't attacked. Otherwise, If the argument e did not attack itself, the grounded extension should be 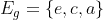 , which is not the case.
, which is not the case.
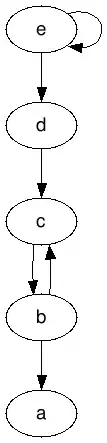
In this last example, the cycle rises to different preferred extensions, where you can use as support the equivalent concept of argument labeling defined elsewhere by Martin Caminada.
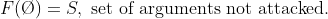
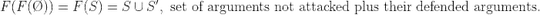

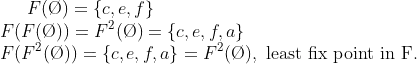

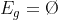 , since There aren't arguments that weren't attacked. Otherwise, If the argument e did not attack itself, the grounded extension should be
, since There aren't arguments that weren't attacked. Otherwise, If the argument e did not attack itself, the grounded extension should be 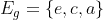 , which is not the case.
, which is not the case.