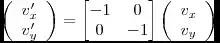I have a column X which is full of floats with decimals places ranging from 0 (no decimals) to 6 (maximum). I can count on the fact that there are no floats with greater than 6 decimal places. Given that, how do I make a new column such that it tells me how many digits come after the decimal?
I have seen some threads suggesting that I use CAST to convert the float to a string, then parse the string to count the length of the string that comes after the decimal. Is this the best way to go?
You can use something like this:
declare @v sql_variant
set @v=0.1242311
select SQL_VARIANT_PROPERTY(@v, 'Scale') as Scale
This will return 7.
I tried to make the above query work with a float column but couldn't get it working as expected. It only works with a sql_variant column as you can see here: http://sqlfiddle.com/#!6/5c62c/2
So, I proceeded to find another way and building upon this answer, I got this:
SELECT value,
LEN(
CAST(
CAST(
REVERSE(
CONVERT(VARCHAR(50), value, 128)
) AS float
) AS bigint
)
) as Decimals
FROM Numbers
Here's a SQL Fiddle to test this out: http://sqlfiddle.com/#!6/23d4f/29
To account for that little quirk, here's a modified version that will handle the case when the float value has no decimal part:
SELECT value,
Decimals = CASE Charindex('.', value)
WHEN 0 THEN 0
ELSE
Len (
Cast(
Cast(
Reverse(CONVERT(VARCHAR(50), value, 128)) AS FLOAT
) AS BIGINT
)
)
END
FROM numbers
Here's the accompanying SQL Fiddle: http://sqlfiddle.com/#!6/10d54/11
This thread is also using CAST, but I found the answer interesting:
http://www.sqlservercentral.com/Forums/Topic314390-8-1.aspx
DECLARE @Places INT
SELECT TOP 1000000 @Places = FLOOR(LOG10(REVERSE(ABS(SomeNumber)+1)))+1
FROM dbo.BigTest
and in ORACLE:
SELECT FLOOR(LOG(10,REVERSE(CAST(ABS(.56544)+1 as varchar(50))))) + 1 from DUAL
A float is just representing a real number. There is no meaning to the number of decimal places of a real number. In particular the real number 3 can have six decimal places, 3.000000, it's just that all the decimal places are zero.
You may have a display conversion which is not showing the right most zero values in the decimal.
Note also that the reason there is a maximum of 6 decimal places is that the seventh is imprecise, so the display conversion will not commit to a seventh decimal place value.
Also note that floats are stored in binary, and they actually have binary places to the right of a binary point. The decimal display is an approximation of the binary rational in the float storage which is in turn an approximation of a real number.
So the point is, there really is no sense of how many decimal places a float value has. If you do the conversion to a string (say using the CAST) you could count the decimal places. That really would be the best approach for what you are trying to do.
I answered this before, but I can tell from the comments that it's a little unclear. Over time I found a better way to express this.
Consider pi as
(a) 3.141592653590
This shows pi as 11 decimal places. However this was rounded to 12 decimal places, as pi, to 14 digits is
(b) 3.1415926535897932
A computer or database stores values in binary. For a single precision float, pi would be stored as
(c) 3.141592739105224609375
This is actually rounded up to the closest value that a single precision can store, just as we rounded in (a). The next lowest number a single precision can store is
(d) 3.141592502593994140625
So, when you are trying to count the number of decimal places, you are trying to find how many decimal places, after which all remaining decimals would be zero. However, since the number may need to be rounded to store it, it does not represent the correct value.
Numbers also introduce rounding error as mathematical operations are done, including converting from decimal to binary when inputting the number, and converting from binary to decimal when displaying the value.
You cannot reliably find the number of decimal places a number in a database has, because it is approximated to round it to store in a limited amount of storage. The difference between the real value, or even the exact binary value in the database will be rounded to represent it in decimal. There could always be more decimal digits which are missing from rounding, so you don't know when the zeros would have no more non-zero digits following it.
Solution for Oracle but you got the idea. trunc() removes decimal part in Oracle.
select *
from your_table
where (your_field*1000000 - trunc(your_field*1000000)) <> 0;
The idea of the query: Will there be any decimals left after you multiply by 1 000 000.
Another way I found is
SELECT 1.110000 , LEN(PARSENAME(Cast(1.110000 as float),1)) AS Count_AFTER_DECIMAL
I've noticed that Kshitij Manvelikar's answer has a bug. If there are no decimal places, instead of returning 0, it returns the total number of characters in the number.
So improving upon it:
Case When (SomeNumber = Cast(SomeNumber As Integer)) Then 0 Else LEN(PARSENAME(Cast(SomeNumber as float),1)) End
Here's another Oracle example. As I always warn non-Oracle users before they start screaming at me and downvoting etc... the SUBSTRING and INSTRING are ANSI SQL standard functions and can be used in any SQL. The Dual table can be replaced with any other table or created. Here's the link to SQL SERVER blog whre i copied dual table code from: http://blog.sqlauthority.com/2010/07/20/sql-server-select-from-dual-dual-equivalent/
CREATE TABLE DUAL
(
DUMMY VARCHAR(1)
)
GO
INSERT INTO DUAL (DUMMY)
VALUES ('X')
GO
The length after dot or decimal place is returned by this query. The str can be converted to_number(str) if required. You can also get the length of the string before dot-decimal place - change code to LENGTH(SUBSTR(str, 1, dot_pos))-1 and remove +1 in INSTR part:
SELECT str, LENGTH(SUBSTR(str, dot_pos)) str_length_after_dot FROM
(
SELECT '000.000789' as str
, INSTR('000.000789', '.')+1 dot_pos
FROM dual
)
/
SQL>
STR STR_LENGTH_AFTER_DOT
----------------------------------
000.000789 6
You already have answers and examples about casting etc...
This question asks of regular SQL, but I needed a solution for SQLite. SQLite has neither a log10 function, nor a reverse string function builtin, so most of the answers here don't work. My solution is similar to Art's answer, and as a matter of fact, similar to what phan describes in the question body. It works by converting the floating point value (in SQLite, a "REAL" value) to text, and then counting the caracters after a decimal point.
For a column named "Column" from a table named "Table", the following query will produce a the count of each row's decimal places:
select
length(
substr(
cast(Column as text),
instr(cast(Column as text), '.')+1
)
) as "Column-precision" from "Table";
The code will cast the column as text, then get the index of a period (.) in the text, and fetch the substring from that point on to the end of the text. Then, it calculates the length of the result.
Remember to limit 100 if you don't want it to run for the entire table!
It's not a perfect solution; for example, it considers "10.0" as having 1 decimal place, even if it's only a 0. However, this is actually what I needed, so it wasn't a concern to me.
Hopefully this is useful to someone :)
Probably doesn't work well for floats, but I used this approach as a quick and dirty way to find number of significant decimal places in a decimal type in SQL Server. Last parameter of round function if not 0 indicates to truncate rather than round.
CASE
WHEN col = round(col, 1, 1) THEN 1
WHEN col = round(col, 2, 1) THEN 2
WHEN col = round(col, 3, 1) THEN 3
...
ELSE null END
