I have a set of nodes A-G, Z, with weighted edges defined, where A-G are various nodes in a funnel, with Z at the very bottom.
Visualize a funnel (V-shaped) with various edges, but eventually pointed towards Z, the final node, like water flowing down to a single point Z. We want to find the cheapest path down to Z which covers all nodes in the funnel.
Here are the constraints:
- There are no orphaned nodes (all nodes are connected/included)
- We want to minimize the sum of the weighted edges
- "Sharing edges", like water merging as it flows downwards, only counts the shared edge's weight once (in other words, it's free to flow down a wet path)
Which boost graph algorithm should I use to find the optimal set of edges for this problem?
- A-B-D-E-Z is a cheap path that covers a lot of nodes
- C-G-Z is a bit forced as G only has one path to Z
- F-Z looks cheap, but then we notice that since C-G-Z is forced, F-G-Z is actually cheaper than F-Z (since we don't need to double-count the G-Z segment, the incremental cost of F-G is only 1)
So, the set of edges should be (A-B, B-D, D-E, E-Z, C-G, F-G, G-Z)
I am certain this is not a new problem: I just don't know enough graph theory to identify/name the algorithm.

Update
While researching the problem some more, I found that if the graph were not directed, the problem is reduced to a Minimum Spanning Tree. In other words, if we did not specify, a priori, that Z is the lowest point in the graph (through the use of arrows), and water were allowed to flow in both directions (generally true, unless we have valves), then this second model will work fine.
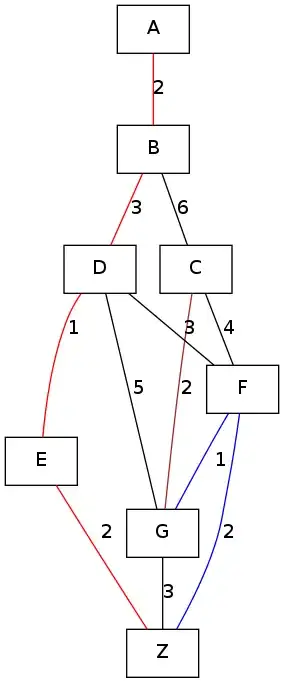
Of course, instead of being forced to use the old the G-Z directed edge, we can now choose the new F-Z undirected edge for a smaller weight.
In light of these results, if we truly need the edges to be directed, liori's answer is the best response for the original question (ie an algorithm needs to be coded).
Output
D <--> E with weight of 1
F <--> G with weight of 1
A <--> B with weight of 2
E <--> Z with weight of 2
C <--> G with weight of 2
F <--> Z with weight of 2
B <--> D with weight of 3
Total Weight = 13
Code for Undirected Acyclic Graph, using a Minimum Spanning Tree
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/kruskal_min_spanning_tree.hpp>
#include <iostream>
int
main()
{
using namespace boost;
typedef adjacency_list < vecS, vecS, undirectedS,
no_property, property < edge_weight_t, int > > Graph;
typedef graph_traits < Graph >::edge_descriptor Edge;
typedef graph_traits < Graph >::vertex_descriptor Vertex;
typedef std::pair<int, int> E;
char letter[] = "ABCDEFGZ";
const int num_nodes = 8;
E edge_array[] = {
E(0,1), E(1,2), E(1,3), E(3,6), E(3,5), E(3,4), E(2,5), E(2,6),
E(5,7), E(5,6), E(6,7), E(4,7)
};
int weights[] = { 2, 6, 3, 5, 3, 1, 4, 2, 2, 1, 3, 2 };
std::size_t num_edges = sizeof(edge_array) / sizeof(E);
Graph g(edge_array, edge_array + num_edges, weights, num_nodes);
property_map < Graph, edge_weight_t >::type weight = get(edge_weight, g);
std::vector < Edge > spanning_tree;
kruskal_minimum_spanning_tree(g, std::back_inserter(spanning_tree));
int total_weight = 0;
for (std::vector < Edge >::iterator ei = spanning_tree.begin();
ei != spanning_tree.end(); ++ei)
{
std::cout << letter[source(*ei, g)] << " <--> " << letter[target(*ei, g)]
<< " with weight of " << weight[*ei]
<< std::endl;
total_weight += weight[*ei];
}
std::cout << "Total Weight = " << total_weight << std::endl;
return EXIT_SUCCESS;
}