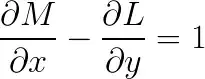7

I have a bunch of images like this one:

enter image description here

The corresponding data is not available. I need to automatically retrieve about 100 points (regularly x-spaced) on the blue curve. All curves are very similar, so I need at least 1 pixel precision, but sub-pixel would be preferred. The good news is all curves start from 0,0 and end at 1,1, so we may forget about the grid.

Any hint on Python libs that could help or any other approach ? Thanks !

CharlesB
  • 86,532
  • 28
  • 194
  • 218
Dr. Goulu
  • 580
  • 7
  • 21

2 Answers2

6

I saved your image to a file 14154233_input.png. Then this program

import pylab as plt
import numpy as np

# Read image from disk and filter all grayscale
im = plt.imread("14154233_input.png")[:,:,:3]
im -= im.mean(axis=2).reshape(im.shape[0], im.shape[1], 1).repeat(3,axis=2)
im_maxnorm = im.max(axis=2)

# Find y-position of remaining line
ypos = np.ones((im.shape[1])) * np.nan
for i in range(im_maxnorm.shape[1]):
    if im_maxnorm[:,i].max()<0.01:
        continue
    ypos[i] = np.argmax(im_maxnorm[:,i])

# Pick only values that are set
ys = 1-ypos[np.isfinite(ypos)]
# Normalize to 0,1
ys -= ys.min()
ys /= ys.max()

# Create x values
xs = np.linspace(0,1,ys.shape[0])

# Create plot of both 
# read and filtered image and
# data extracted
plt.figure(figsize=(4,8))
plt.subplot(211)
plt.imshow(im_maxnorm)
plt.subplot(212, aspect="equal")
plt.plot(xs,ys)
plt.show()

Produces this plot:

Ausgabe

You can then do with xs and ys whatever you want. Maybe you should put this code in a function that returns xs and ys or so.

One could improve the precision by fitting gaussians on each column or so. If you really need it, tell me.

Thorsten Kranz
  • 12,492
  • 2
  • 39
  • 56
  • I'm not practical with pylab, can I ask you to explain how the `im -= im.mean(axis=2).reshape(im.shape[0], im.shape[1], 1).repeat(3,axis=2)` line works? – Coffee on Mars Jan 04 '13 at 10:25
  • Sure. imread gives us an RGBA image, i.e., our array has shape (x,y,4), which I immediately reduce by discarding alpha ([:,:,:3] in previous line). I then wanted to set all colors with red=green=blue (all grays from black to white) to black, so that only the blue line remains. I do this by subtracting, for every pixel, the average of the R, G and B-values from each of them. If they are equal, all become zero. `.mean(axis=2)` calculates the average, making a 2d-array; `.reshape()` makes it 3d again, by just adding a 3. dim of len 1; `.repeat()` resets the shape of the array to that of `im` – Thorsten Kranz Jan 04 '13 at 10:30
1

First, read the image via

from scipy.misc import imread    
im = imread("thefile.png")

This gives a 3D numpy array with the third dimension being the color channels (RGB+alpha). The curve is in the blue channel, but the grid is there also. But in the red channel, you have the grid and not the curve. So we use

a = im[:,:,2] - im[:,:,0]

Now, we want the position of the maximum along each column. With one pixel precision, it is given by

y0 = np.argmax(a, axis=0)

The result of this is zero when there is no blue curve in the column , i.e. outside the frame. On can get the limits of the frame by

xmin, xmax = np.where(y0>0)[0][[0,-1]

With this, you may be able to rescale x axis.

Then, you want subpixel resolution. Let us focus on a single column

f=a[:,x]

We use a single iteration of the Newton method to refine the position of an extrema

y1 = y0 - f'[y]/f''[y]

Note that we cannot iterate further because of the discreet sampling. Nontheless, we want a good approximation of the derivatives, so we will use a 5-point scheme for both.

coefprime = np.array([1,-8, 0, 8, -1], float)
coefsec = np.array([-1, 16, -30, 16, -1], float)
y1 = y0 - np.dot(f[y0-2:y0+3], coefprime)/np.dot(f[y0-2:y0+3], coefsec)

P.S. : Thorsten Kranz was faster than me (at least here), but my answer has the subpixel precision and my way of extracting the blue curve is probably more understandable.

Mathieu Leocmach
  • 19
  • 1