I want to detect and COMPLETE all possible quadrilateral shapes from randomly located line segments!
The photo attached is an example, the lines might always appear in very different locations.
Anyone can point out any good algorithm for this?
The solution is to detect and predict the yellow quadrilateral
In the case of 11 line segments, you have 330 ways of choosing four segments. You could determine the likelihood of each combination making a quadrilateral, and grade that way.
It is possible to have a Hough transform detect forms other than lines, though it becomes harder to visualise as the accumulator space would require more than two dimensions. Circles can be found in three dimensions (midX, midY, radius), ellipses in four (I believe). I'm not sure exactly how few parameters you'd need to model a quadrilateral, and I believe that the performance of the Hough transform starts to drop off when you get higher than three dimensions. The accumulator space becomes so large that the noise ratio increases significantly.
Here's a related question that may have some interesting answers for you.
Let us know how you get on!
I took a stab at this problem today, and uploaded my solution to GitHub. There is too much code to post here.
Here's a screenshot showing the output:
The solution I took is basically what I described above before this edit.
The evaluation works by calculating a crude error score. This is the sum of two different types of error:
The second type of error could possibly be determined in a more robust way. It was necessary to find a solution for your sample data set.
I haven't experimented with other data sets. It may need some tweaking to make it more robust. I have tried to avoid using too many parameters so that it should be straightforward to adjust to a particular environment. For example to control sensitivity to occlusion, as seen in your sample image.
It finds the solution in about 160ms on my laptop. However I haven't made any performance optimisations. I expect that the methods of finding combinations/permutations could be significantly optimised if you needed this to run closer to real-time, as is often the case with computer vision experiments.
About any four lines can be completed to form a quadrilateral if you don't impose constraints on angles etc.
Image with potentially wrong quadrilaterals:
Probably you don't want to include quadrilaterals like the yellow one shown in my example. You should have constraints on angles, minimum/maximum size, aspect ratio and the degree of completion allowed. If 90 percent of the lines have to be added in order to form a complete quadrilateral this would probably not be a very good candidate.
I fear that you will have to test every possible combination of lines and apply a heuristic on them to give them points. Many points for angles close to 90 degrees (if what you want are rectangles), for completeness, for aspect ratios close to the expected one etc.
UPDATE
Using a point system has advantages over just applying strict rules.
Let's say you have a strict rule (in pseudo code):
(angles == 90 +/- 10 degrees) && (line_completeness>50%)
This would work, can however lead to situations like angles == 90 +/- 1 degree) && (line_completeness == 45%). According to the rules this quadrilateral would not pass because of the poor line completeness; however, the quality of the angles is exceptional, still making it a very good candidate.
It is better to give points. Say 20 points for an angle of exactly 90 degrees, falling to 0 points for an angle of 90 +/-15 degrees and 10 points for complete lines towards 0 points for lines complete by only 25% for instance. This makes angles more important than line completeness and also creates softer conditions for a problem that does not have absolute rules.
I don't use C# so you will have to translate the code. The following code is in Java. I tested it with the included test case. I don't know how to add attachment to stackoverflow yet, so I am including the actual code here.
There are four classes (ShapeFinder, Line, Point, and Quadrilateral) and one test class (ShapeFinderTest):
ShapeFinder class:
package stackoverflow;
import java.util.ArrayList;
import java.util.List;
public class ShapeFinder {
private List<Line> lines;
private List<Quadrilateral> allQuadrilaterals;
/*
* I am assuming your segments are in a list of arrays:
* [{{x1,y1,},{x2,y2}}, {{x1,y1,},{x2,y2}}, {{x1,y1,},{x2,y2}}]
* You can change this.
*
* So basically you call ShapeFinder with a list of your line segments.
*/
public ShapeFinder(List<Double[][]> allSegments) {
lines = new ArrayList<Line>(allSegments.size());
allQuadrilaterals = new ArrayList<Quadrilateral>();
for (Double[][] segment : allSegments) {
addSlopeInterceptForm(segment);
}
}
/**
* You call this function to compute all possible quadrilaterals for you.
*/
public List<Quadrilateral> completeQuadrilaterals() {
for (int w = 0; w < lines.size(); w++) {
for (int x = w + 1; x < lines.size(); x++) {
for (int y = x + 1; y < lines.size(); y++) {
for (int z = y + 1; z < lines.size(); z++) {
addQuadrilateral(w, x, y, z);
}
}
}
}
return allQuadrilaterals;
}
//assume {{x1,y1,},{x2,y2}}
private void addSlopeInterceptForm(Double[][] s) {
double x1 = s[0][0];
double y1 = s[0][1];
double x2 = s[1][0];
double y2 = s[1][1];
double m = (y1 - y2) / (x1 - x2);
double b = y2 - m * x2;
if (isInfinityOrNaN(m)) {
m = Double.NaN;
b = x1;
}
lines.add(new Line(m, b));
}
/*
* Given four lines, this function creates a quadrilateral if possible
*/
private void addQuadrilateral(int w, int x, int y, int z) {
Point wx = intersect(w, x);
Point wy = intersect(w, y);
Point wz = intersect(w, z);
Point xy = intersect(x, y);
Point xz = intersect(x, z);
Point yz = intersect(y, z);
if (notNull(wx) && notNull(xy) && notNull(yz) && notNull(wz) && isNull(wy) && isNull(xz)) {
allQuadrilaterals.add(new Quadrilateral(wx, xy, yz, wz));
}
}
private Point intersect(int c, int d) {
double m1 = lines.get(c).slope;
double b1 = lines.get(c).intercept;
double m2 = lines.get(d).slope;
double b2 = lines.get(d).intercept;
double xCor, yCor;
if ((isInfinityOrNaN(m1) && !isInfinityOrNaN(m2)) || (!isInfinityOrNaN(m1) && isInfinityOrNaN(m2))) {
xCor = isInfinityOrNaN(m1) ? b1 : b2;
yCor = isInfinityOrNaN(m1) ? m2 * xCor + b2 : m1 * xCor + b1;;
} else {
xCor = (b2 - b1) / (m1 - m2);
yCor = m1 * xCor + b1;
}
if (isInfinityOrNaN(xCor) || isInfinityOrNaN(yCor)) {
return null;
}
return new Point(xCor, yCor);
}
private boolean isInfinityOrNaN(double d){
return Double.isInfinite(d)||Double.isNaN(d);
}
private boolean notNull(Point p) {
return null != p;
}
private boolean isNull(Point p) {
return null == p;
}
}
Line class:
package stackoverflow;
public class Line {
double slope;
double intercept;
public Line(double slope, double intercept) {
this.slope = slope;
this.intercept = intercept;
}
}
Point class:
package stackoverflow;
class Point {
double xCor;
double yCor;
public Point(double xCor, double yCor) {
this.xCor = xCor;
this.yCor = yCor;
}
public String toString(){
return "("+xCor+","+yCor+")";
}
}
Quadrilateral class:
package stackoverflow;
public class Quadrilateral {
private Point w, x, y, z;
public Quadrilateral(Point w, Point x, Point y, Point z) {
this.w = w;
this.x = x;
this.y = y;
this.z = z;
}
public String toString() {
return "[" + w.toString() + ", " + x.toString() + ", " + y.toString() + ", " + z.toString() + "]";
}
}
UNIT TEST:
package stackoverflow;
import java.util.ArrayList;
import java.util.List;
import org.junit.Test;
public class ShapeFinderTest {
@Test
public void testCompleteQuadrilaterals() {
List<Double[][]> lines = new ArrayList<>();
lines.add(new Double[][]{{2., 5.}, {6., 5.}});
lines.add(new Double[][]{{2., 1.}, {2., 5.}});
lines.add(new Double[][]{{2., 1.}, {6., 1.}});
lines.add(new Double[][]{{6., 5.}, {6., 1.}});
lines.add(new Double[][]{{0., 0.}, {5., 1.}});
lines.add(new Double[][]{{5., 5.}, {10., 25.}});
ShapeFinder instance = new ShapeFinder(lines);
List<Quadrilateral> result = instance.completeQuadrilaterals();
for (Quadrilateral q : result) {
System.out.println(q.toString());
}
}
}
From the examples, I assume the question is more along the lines of Find all quadrilaterals that have a line contained completely within each of its sides. This is not at all clear from the explanation provided.
Below is some reasonably easy-to-implement pseudo-code. Now just to create an efficient data-structure to prevent the O(N^4) complexity. Maybe sort lines by position or gradient.
i,j,k,l are as follows:
l
|---|
j| |k
|---|
i
extendIntersect is merely a function that extends the 2 lines into infinity (or to whichever bounds you choose) and return the point where they intersect, easy to do mathematically.
onLine returns true if a point lies on a line.
onSameSide returns true if both points lie on the same side of a line
for (Line i = lines[0]:lines[lineCount])
for (Line j = lines[1]:lines[lineCount])
Point ijIntersect = extendIntersect(i, j)
if (ijIntersect == NULL || onLine(ijIntersect, i) || onLine(ijIntersect, j))
continue;
for (Line k = lines[2]:lines[lineCount])
Point ikIntersect = extendIntersect(i, k)
if (ikIntersect == NULL || onLine(ikIntersect, i) || onLine(ikIntersect, k) ||
onSameSide(ijIntersect, ikIntersect, i)) continue
for (Line l = lines[3]:lines[lineCount])
Point jlIntersect = extendIntersect(j, l)
Point klIntersect = extendIntersect(k, l)
if (jlIntersect == NULL || onLine(jlIntersect, j) || onLine(jlIntersect, l) ||
klIntersect == NULL || onLine(klIntersect, k) || onLine(klIntersect, l) ||
onSameSide(jlIntersect, ijIntersect, j) ||
onSameSide(klIntersect, ikIntersect, k)) continue
printQuad(ijIntersect, ikIntersect, klIntersect, jlIntersect)
Some sort of error checking as Drew Noakes suggested might also be a good idea.
Solution 1:
Here is a complete solution written in python 2.7.x using OpenCV 2.4 and Sympy.
I used the data (line segments) from D.Noakes, but I took a different approach.
Problem definition:
For a set of line segments, find all the possible quadrilateral shapes where the segments fit inside the edges of the quad.
Method:
Result:
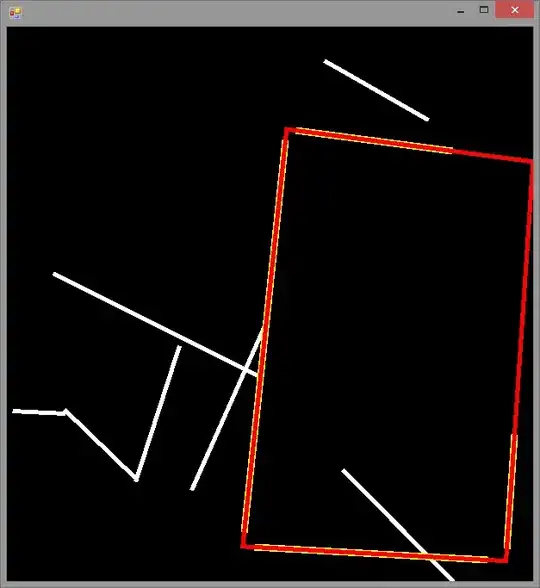
This method detects 4 quadrilateral shapes in the image
See animated GIF: https://ibb.co/4Rv9rJW
Code: https://pastiebin.com/5f3836269f7e5
#!/usr/bin/env python
"""
Find Quads:
For a set of line segments, find all the possible
quadrilateral shapes where the segments fit
inside the edges of the quad.
Dependencies:
Sympy is used for geometry primitives.
sudo pip install sympy
"""
import numpy as np
import cv2
import itertools # combinations, product
from sympy import Point, Line, Segment, convex_hull
import sys
input_image = cv2.imread("detected_lines.jpg")
#------------------------------------------------------------------------------#
def checkPointInImage(point, image_width, image_height):
"""
Check if a Sympy Point2D is within the bounds of an OpenCV image.
"""
pt_x = int(round(point.x))
pt_y = int(round(point.y))
if (pt_x >= 0) and (pt_x < image_width) and (pt_y >= 0) and (pt_y < image_height):
return True
# Point is outside the image boundary
return False
def checkPointsInImage(points, image_width, image_height):
"""
Check if a set of Sympy Point2D are all within the bounds of an OpenCV image.
"""
for point in points:
if not checkPointInImage(point, image_width, image_height):
return False
# All points are within the image boundary
return True
def getUniquePairs(segments, image_dims):
"""
Get all the possible pairs of line segments.
(the unique combinations of 2 lines)
Note: this doesn't check for duplicate elements, it works
only on the position in the list.
"""
# Check that a pair of segments are not intersecting
check_segments_dont_intersect = True
# Check that the endpoint of one segment
# does not touch the other segment (within 10 pixels)
check_segment_endpoints = True
endpoint_min_separation = 10
# Project the segments and check if the intersection
# point is within the image
check_projected_segments_dont_intersect = True
pairs = list(itertools.combinations(segments, 2)) # a list of tuple
image_width, image_height = image_dims
filtered_pairs = []
for pair in pairs:
segment1 = pair[0]
segment2 = pair[1]
if check_segments_dont_intersect:
if bool(len(segment1.intersection(segment2))):
# Discard this pair.
# The pair of segments intersect each other.
continue
if check_segment_endpoints or check_projected_segments_dont_intersect:
line1 = Line(segment1)
line2 = Line(segment2)
intersection_points = line1.intersection(line2)
intersects = bool(len(intersection_points))
if intersects:
intersection_point = intersection_points[0]
if check_segment_endpoints:
# Measure the distance from the endpoint of each segment
# to the intersection point.
d1 = float(segment1.points[0].distance(intersection_point))
d2 = float(segment1.points[1].distance(intersection_point))
d3 = float(segment2.points[0].distance(intersection_point))
d4 = float(segment2.points[1].distance(intersection_point))
d = np.array([d1,d2,d3,d4])
if (d < float(endpoint_min_separation)).any():
# Discard this pair.
# One segment is (almost) touching the other.
continue
if check_projected_segments_dont_intersect:
if checkPointInImage(intersection_point, image_width, image_height):
# Discard this pair.
# After projecting the segments as lines,
# they intersect somewhere on the image.
continue
filtered_pairs.append(pair)
return filtered_pairs
def getCombinationsOfTwoLists(list1, list2):
"""
For two sets of Line Segment pairs,
generate all possible combinations.
"""
return list(itertools.product(list1, list2))
def getIntersectionLineSegments(segment1, segment2):
"""
Find the intersection of two line segments,
by extending them into infinite lines.
"""
line1 = Line(segment1)
line2 = Line(segment2)
intersection_points = line1.intersection(line2)
intersects = bool(len(intersection_points))
if intersects:
intersection_point = intersection_points[0]
return intersection_point
# Error, lines do not intersect
print("WARNING: Horizontal and vertical line segments do not intersect.")
print("This should not happen!")
return None
def checkLineSegmentIsAbove(segment1, segment2):
"""
Check if one line segment is above the other.
(this assumes the segments are not intersecting)
"""
# In image coordinates, (+x,+y) is bottom-right corner.
if (segment1.points[0].y > segment2.points[0].y): return False
if (segment1.points[0].y > segment2.points[1].y): return False
if (segment1.points[1].y > segment2.points[0].y): return False
if (segment1.points[1].y > segment2.points[1].y): return False
return True
def checkLineSegmentOnLeft(segment1, segment2):
"""
Check if one line segment is on the left side of the other.
(this assumes the segments are not intersecting)
"""
# In image coordinates, (+x,+y) is bottom-right corner.
if (segment1.points[0].x > segment2.points[0].x): return False
if (segment1.points[0].x > segment2.points[1].x): return False
if (segment1.points[1].x > segment2.points[0].x): return False
if (segment1.points[1].x > segment2.points[1].x): return False
return True
def getConvexIntersectionPoints_method2(horizontal_segment1, horizontal_segment2, vertical_segment1, vertical_segment2):
"""
For two pairs of line segments, treat them as
infinite lines and find the intersection points.
These 4 points are in a clockwise order that
represents a convex quadrilateral.
"""
# Sort the segments in clockwise order
top_segment = None
right_segment = None
bottom_segment = None
left_segment = None
if checkLineSegmentIsAbove(horizontal_segment1, horizontal_segment2):
top_segment = horizontal_segment1
bottom_segment = horizontal_segment2
else:
top_segment = horizontal_segment2
bottom_segment = horizontal_segment1
if checkLineSegmentOnLeft(vertical_segment1, vertical_segment2):
left_segment = vertical_segment1
right_segment = vertical_segment2
else:
left_segment = vertical_segment2
right_segment = vertical_segment1
corner_pt1 = getIntersectionLineSegments(left_segment, top_segment)
corner_pt2 = getIntersectionLineSegments(top_segment, right_segment)
corner_pt3 = getIntersectionLineSegments(right_segment, bottom_segment)
corner_pt4 = getIntersectionLineSegments(bottom_segment, left_segment)
quad_points = [corner_pt1, corner_pt2, corner_pt3, corner_pt4]
sorted_segments = [top_segment, right_segment, bottom_segment, left_segment]
return (quad_points, sorted_segments)
def checkSegmentsOnQuad_method2(sorted_segments, corners):
"""
Check if all 4 line segments are within
the edges of a quadrilateral.
This assumes that the inputs are already matched.
"""
if (len(sorted_segments) != 4) or (len(corners) != 4):
print("ERROR: Expected 4 segments and 4 corners in checkSegmentsOnQuad_method2()")
sys.exit()
# Get the 4 edges
edges = []
for i in range(3):
p1 = corners[i]
p2 = corners[i+1]
edges.append(Segment(p1, p2))
p1 = corners[3]
p2 = corners[0]
edges.append(Segment(p1, p2))
for i in range(4):
if not edges[i].contains(sorted_segments[i]):
return False
return True
def getQuads(sets_of_four_segments, image_dims):
"""
Find quadrilateral shapes.
"""
image_width, image_height = image_dims
quads = []
for i in range(len(sets_of_four_segments)):
# Determine if 4 line segments represent
# a valid quadrilateral shape:
segments = sets_of_four_segments[i]
horizontal_segment1 = segments[0][0]
horizontal_segment2 = segments[0][1]
vertical_segment1 = segments[1][0]
vertical_segment2 = segments[1][1]
quad_points, sorted_segments = getConvexIntersectionPoints_method2(horizontal_segment1, horizontal_segment2, vertical_segment1, vertical_segment2)
if not checkPointsInImage(quad_points, image_width, image_height):
print(" Bad quad, an intersection point (one corner of the quad) is outside image!")
# Save debug image
img = np.copy(input_image)
drawCrosshairs(img, quad_points)
drawQuad(img, quad_points)
suffix = str(i).zfill(2)
cv2.imwrite("candidate_quad_"+suffix+".jpg", img)
# Discard this quad.
# A corner point is outside the image boundary.
continue
# Check if each line segment is within one side of the quad.
# - The segments can not intersect each other.
# - The end of a segment can not extend out past the quad.
# - All segments must be contained within one edge of the shape.
if checkSegmentsOnQuad_method2(sorted_segments, quad_points):
print(" Good")
quads.append(quad_points)
else:
print(" Bad quad, a line segment is not within the quad")
# Save debug image
img = np.copy(input_image)
drawCrosshairs(img, quad_points)
drawQuad(img, quad_points)
suffix = str(i).zfill(2)
cv2.imwrite("candidate_quad_"+suffix+".jpg", img)
#cv2.imshow("Quad corners", img)
#cv2.waitKey()
return quads
#------------------------------------------------------------------------------#
# Drawing functions:
def drawSegment(image, segment, color):
"""
Draw a Sympy Line Segment on an OpenCV image.
"""
thickness = 2
x1 = int(segment.points[0].x) # should already be int
y1 = int(segment.points[0].y)
x2 = int(segment.points[1].x)
y2 = int(segment.points[1].y)
cv2.line(image, (x1,y1), (x2,y2), color, thickness)
def drawSegments(image, segments, color=(0,0,255)):
"""
Draw lines on an OpenCV image.
Default color is red.
"""
for segment in segments:
drawSegment(image, segment, color)
def drawCrosshair(image, point):
"""
Draw a Sympy Point2D on an OpenCV image
with a cross marker.
"""
pt_x = int(round(point.x))
pt_y = int(round(point.y))
length = 5
thickness = 2
color = (255,0,255) # magenta
cv2.line(image, (pt_x, pt_y-length), (pt_x, pt_y+length), color, thickness)
cv2.line(image, (pt_x-length, pt_y), (pt_x+length, pt_y), color, thickness)
def drawCrosshairs(image, points):
"""
Draw marks on an OpenCV image.
"""
for point in points:
drawCrosshair(image, point)
def drawQuad(image, corners, color=(0,255,0)):
"""
Draw a quadrilateral shape.
The 4 corner points are Sympy Point2D.
"""
for i in range(len(corners)-1):
p1 = corners[i]
p2 = corners[i+1]
segment = Segment(p1, p2)
drawSegment(image, segment, color)
# Close the polygon
p1 = corners[len(corners)-1]
p2 = corners[0]
segment = Segment(p1, p2)
drawSegment(image, segment, color)
#------------------------------------------------------------------------------#
if input_image == None:
print("ERROR: Can't find input image")
sys.exit()
#cv2.imshow("input_image", input_image)
#cv2.waitKey()
# Line segments sample data
segment1 = Segment(Point(335,120), Point(517,144))
segment2 = Segment(Point(287, 604), Point(558, 619))
segment3 = Segment(Point(323, 131), Point(275, 587))
segment4 = Segment(Point(589, 473), Point(580, 606))
segment5 = Segment(Point(368, 39), Point(489, 108))
segment6 = Segment(Point(53, 286), Point(293, 406))
segment7 = Segment(Point(299, 347), Point(214, 538))
segment8 = Segment(Point(200, 370), Point(149, 528))
segment9 = Segment(Point(6, 446), Point(68, 449))
segment10 = Segment(Point(66, 444), Point(150, 525))
segment11 = Segment(Point(389, 514), Point(518, 644))
segments = [segment1, segment2, segment3, segment4, segment5, segment6, segment7, segment8, segment9, segment10, segment11]
image_width = input_image.shape[1]
image_height = input_image.shape[0]
image_dims = (image_width, image_height)
input_image_with_segments = np.copy(input_image)
drawSegments(input_image_with_segments, segments)
cv2.imshow("input_image_with_segments", input_image_with_segments)
cv2.waitKey()
# Sort the line segments into 2 groups:
horizontal_segments = []
vertical_segments = []
image_width = input_image.shape[1]
x_axis = Line((0, 0), (image_width, 0))
for segment in segments:
# Compute the angle of each line segment.
# Angle is w.r.t. the top edge of the image
# in a clockwise direction.
angle = float(x_axis.angle_between(segment))
# Check 315 to 360 degrees
if (angle >= 2.0*np.pi-np.pi/4.0) and (angle <= 2.0*np.pi):
horizontal_segments.append(segment)
# Check 0 to 45 degrees
elif (angle >= 0.0) and (angle < np.pi/4.0):
horizontal_segments.append(segment)
# Check 135 to 225 degrees
elif (angle > np.pi-np.pi/4.0) and (angle < np.pi+np.pi/4.0):
horizontal_segments.append(segment)
else:
vertical_segments.append(segment)
# Save debug images
input_image_with_horizontal_segments = np.copy(input_image)
drawSegments(input_image_with_horizontal_segments, horizontal_segments)
cv2.imwrite("segments_horizontal.jpg", input_image_with_horizontal_segments)
input_image_with_vertical_segments = np.copy(input_image)
drawSegments(input_image_with_vertical_segments, vertical_segments)
cv2.imwrite("segments_vertical.jpg", input_image_with_vertical_segments)
# Get all the possible pairs of horizontal line segments:
pairs_of_horizontal_line_segments = getUniquePairs(horizontal_segments, image_dims)
print("Got %d pairs of horizontal line segments" % len(pairs_of_horizontal_line_segments)) # 15 pairs, 10 after filtering
# Get all the pairs of vertical line segments:
pairs_of_vertical_line_segments = getUniquePairs(vertical_segments, image_dims)
print("Got %d pairs of vertical line segments" % len(pairs_of_vertical_line_segments)) # 10 pairs, 6 after filtering
# Save debug images
for i in range(len(pairs_of_horizontal_line_segments)):
pair = pairs_of_horizontal_line_segments[i]
segments = [pair[0], pair[1]]
img = np.copy(input_image)
drawSegments(img, segments)
suffix = str(i).zfill(2)
cv2.imwrite("segment_pairs_horizontal_"+suffix+".jpg", img)
#cv2.imshow("Pair of segments", img)
#cv2.waitKey()
for i in range(len(pairs_of_vertical_line_segments)):
pair = pairs_of_vertical_line_segments[i]
segments = [pair[0], pair[1]]
img = np.copy(input_image)
drawSegments(img, segments)
suffix = str(i).zfill(2)
cv2.imwrite("segment_pairs_vertical_"+suffix+".jpg", img)
#cv2.imshow("Pair of segments", img)
#cv2.waitKey()
# Get all combinations of 4 line segments:
sets_of_four_line_segments = getCombinationsOfTwoLists(pairs_of_horizontal_line_segments, pairs_of_vertical_line_segments)
print("Got %d potential quadrilaterals" % len(sets_of_four_line_segments)) # = 60
# Find the valid quadrilateral shapes:
quads = getQuads(sets_of_four_line_segments, image_dims)
print("Got %d valid quads" % len(quads))
for i in range(len(quads)):
img = np.copy(input_image)
drawQuad(img, quads[i])
# Save result images
suffix = str(i).zfill(2)
cv2.imwrite("quad_"+suffix+".jpg", img)
title = "Candidate Quad " + str(i)
cv2.imshow(title, img)
cv2.waitKey()
