I know this is more high school math(wow been a long time since I was there) but I am trying to solve this programatically so I am reaching out to the collective knowledge of stackoverflow
Given this layout:
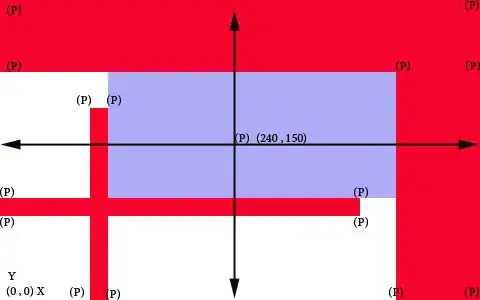
Midpoint is my reference point and in an array I have the vector points of all other points (P)
I can get to this state with code of having the light blue area by breaking it into four quadrants and doing a lame bubble sort to find largest(y) or lowest(x) value in each quadrant.
I need to find only the quadrants that outer border fully hits red no white space. For example the lower left and the up right dont have any white space hitting the light blue rectangle.
I am sure my terminology is all off here and im not looking for any specific code but if someone could point me to a more optimized solution for this problem or the next step in what I already have.
Thank you