6
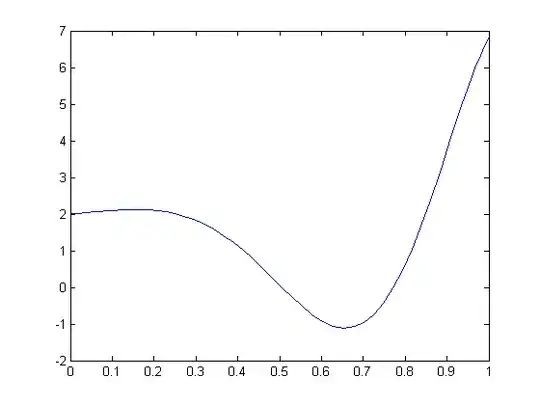
y''' + 41y'' + 360y' + 900y = 600x' + 1200x;
y(0)= 2 ; y'(0)= 1 ; y''(0) = -0.05

How can I solve this equation using the ODE45 function?

I tried this:

==>
function dydt=f(t,y)

dydt = [y(2) ; y(3) ; -41*y(3)-360*y(2)- 900*y(1)]

==>
clear all;

timerange=[0 1.4]; %seconds
initialvalues=[2 1 -0.05];


[t,y]=ode45(@dydt, timerange, initialvalues)

plot(t,y(:,1));

But I need put the X part in the equation - I don't know how...

ag.alessandro
  • 63
  • 1
  • 1
  • 6
  • 1
    What is x' and y'? I first thought that y'=dy(x)/dx, I guess I wrong. If so, this is a partial differential equation (PDE), and ode45 is not the right tool for you... – bla Dec 07 '12 at 01:54
  • y'=dy(t)/dt and x'=dy(t)/dt. y(t) is the output and x(t) is an input signal. – ag.alessandro Dec 07 '12 at 02:23
  • if y'=x' then only use y'! if you want the solution (what you call "output") of y as function of t then I don't understand what si "input signal". your input is the initial conditions... – bla Dec 07 '12 at 03:54
  • I can't use y'=x'. This is a physical system where I apply a signal like x(t)=u(t)(unit step=input) and the system responds with an output, e.g y=123*exp(-5*t)-0.09*exp(-30*t)+1.25*exp(-6*t). The initial conditions are given to find the natural response of the system, without an input. (input function)x(x)-->(system)-->y(t)(output function). Where the "system" is described by the differential equation. The behavior of the system is described by the differential equation. – ag.alessandro Dec 07 '12 at 13:21
  • (input function)x(t)---->(system)---->y(t)(output function) – ag.alessandro Dec 07 '12 at 13:28
  • I found the solution using Laplace transform by hand: Y(s)=[((X(s)(1200+600s)-600x(0))/((s+5)(s+6)(s+30)))]+[((2s^2+83s+761.05)/((s+5)(s+6)(s+30)))], but I need use the Matlab to solve like a differential equation. – ag.alessandro Dec 07 '12 at 13:34
  • Short answer - nest the function f(t,y) below a declaration of x(t) and dx(t) and you can access them. – ccook Dec 07 '12 at 16:53
  • @natan Its an ODE since x != f(y(t)). x=f(t) so that y = f(t). Its just the non-homogenous term wrapped into x – ccook Dec 07 '12 at 17:29

1 Answers1

3

To use ODE45 (or similar) you need to convert the third order ODE into a system of first order ODEs.

To do so, let

y0 = y
y1 = y0'
y2 = y1'
y3 = y2'

Then 

y0' = y1
y1' = y2
y2' = y3

and

y3' = y''' = -41*y2-360y1-900y0+600dx+1200x

you can now use ODE45 to integrate the system by nesting the function where x(t) and dx(t) are available.

function test()

    % some random x function 
    x = @(t) exp(-t);
    dx = @(t) -exp(-t);

    % integrate numerically
    [T, Y] = ode45(@linearized, [0 1], [2 1 -0.05 0]);

    % plot the result
    plot(T, Y(:,1))

    % linearized ode
    function dy = linearized(t,y)
       dy = zeros(4,1);
       dy(1) = y(2);
       dy(2) = y(3);
       dy(3) = y(4);
       dy(4) = -41*y(3)-360*y(2)-900*y(1)+600*dx(t)+1200*x(t);
    end
end

plot

ccook
  • 5,869
  • 6
  • 56
  • 81
  • 1
    As an aside - I realized after the fact you were already linearizing. Just do something like the above to share the functions x, dx – ccook Dec 07 '12 at 16:50
  • This solution is correct. When I describe a x(t) signal the response isn't like the response that I found by the Laplace transform, but this solution is so helpfull. – ag.alessandro Dec 08 '12 at 03:42