What are the maximum and minimum number of nodes in a suffix tree? And how can I prove it?
-
Welcome to Stack Overflow and thanks for posting. Please include some code to show [what you tried](http://whathaveyoutried.com) and have a look at [How to Ask](http://stackoverflow.com/questions/how-to-ask). – Serge Belov Nov 15 '12 at 00:55
-
1This is a duplicate of this question: http://stackoverflow.com/questions/12865639/maximum-and-minimum-number-of-edges-in-a-suffix-tree – Matti John Nov 15 '12 at 00:56
-
That are edges, I want to know it for nodes. There is nothing to implement, I just have to know how many nodes there can be in a suffix tree. – Nov 15 '12 at 01:00
-
1"What are the maximum and minimum number of edges in a suffix tree? And how can I prove it?". You are asking for edges not nodes in your question text, in the title you are asking for nodes.. – Tony Rad Nov 15 '12 at 05:53
-
Just wanted to plug http://cs.stackexchange.com because I think it is even more suited there. – The Unfun Cat Nov 15 '12 at 06:23
-
@TheUnfunCat That's right. To OP: Do let me know if you move the question there. I'd like to move the answer as well. – jogojapan Nov 15 '12 at 06:29
1 Answers
Assuming an input text of N characters in length, the minimum number of nodes, including the root node and all leaf nodes, is N+1, the maximum number of nodes, including the root and leaves, is 2N-1.
Proof of minimum: There must be at least one leaf node for every suffix, and there are N suffixes. There need not be any inner nodes, example: if the text is a sequence of unique symbols, abc$, there are no branches, hence no inner nodes in the resulting suffix tree:
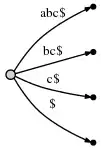
Hence the minimum is N leaves, 0 inner nodes, and 1 root node, in sum N+1 nodes.
Proof of maximum: The number of leaf nodes can never be larger than N, because a leaf node is where a suffix ends, and you can't have more than N distinct suffixes in a string of length N. (In fact, you always have exactly N distinct suffixes, hence N leaf nodes exactly.) The root node is always exactly 1, so the question is what is the maximum number of inner nodes. Every inner node introduces a branch in the tree (because inner nodes of a suffix tree have at least 2 children). Each new branch must eventually lead to at least one extra leaf node, so if you have K inner nodes, there must be at least K+1 leaf nodes, and the presence of the root node requires at least one additional leaf (unless the tree is empty). But the number of leaf nodes is bounded by N, so the maximum number of inner nodes is bounded by N-2. This yields exactly N leaves, 1 root, and a maximum of N-2 inner nodes, 2N-1 in total.
To see that this is not only a theoretical upper bound, but some suffix trees actually reach this maximum, consider as an example a string with just one repeated character: 'aaa$'. Confirm that the suffix tree for this has 7 nodes (including root and leaves):
Summary: As evident, the only real variable is the number of inner nodes; the number of roots and leaves is constant at 1 and N for all suffix trees, while the number of inner nodes varies between 0 and N-2.
- 68,383
- 11
- 101
- 131