You should calculate for each point, whether it is above the line or below. If the line is given in its equation form Ax+By+C, then it is as simple as calculating the sign of this expression, per your point (x,y). If your lines are given in any other form, you should first calculate the form above. (See here and here)
Let L1 be the set of all points below the first line, and L2 the set of all points below the second line. Then, your set is X = Xor(L1,L2)
[  ] Xor [
] Xor [ ]
]
Equals:

Here is a Matlab code that solves you problem for the corner points, based on the solution that I've described. You can adjust the line equations in your code.
function CreateMask()
rows = 100;
cols = 200;
[X,Y] = ndgrid(1:cols,1:rows);
belowFirstLine = X*(1/cols) + Y*(-1/rows) + 0 < 0;
belowSecondLine = X*(-1/cols) + Y*(-1/rows) + 1 < 0;
figure;imshow( transpose(xor(belowSecondLine,belowFirstLine)));
end
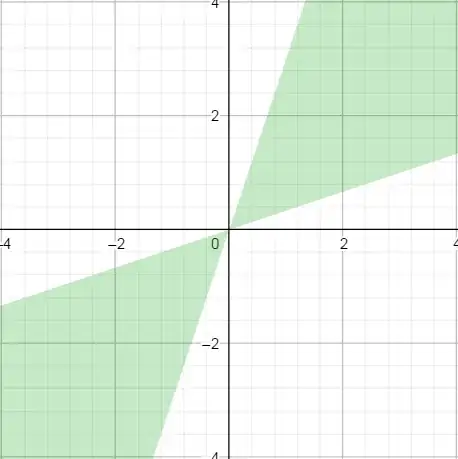
 ] Xor [
] Xor [ ]
] 