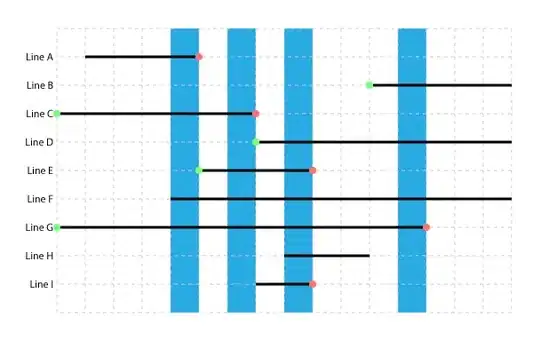
edit: Hierarchy doesn't play nice with my goals here. Leaving original request, but I answered what fulfills the core request (overlap/non-overlap rules) below.
Assume there is some set of 1D lines, each described by 2 unsigned ints: start and end, with start < end. I want to create groups based on if they overlap, but I don't want groups to contain any lines that don't overlap. In the case of a line being in multiple groups, I guess I'll need some sort of hierarchy structure to track groups in groups in groups...
Here's the rules:
- Lines that overlap must be grouped together as low on the hierarchy as possible.
- Lines that don't overlap can't be in the same group.
Anyway, here's an example picture:
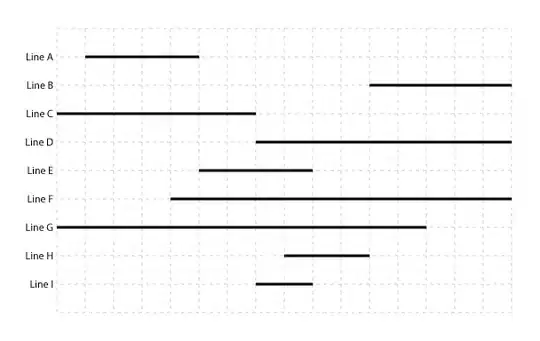
From a quick look, I can say that Line A and Line C form Group 0, Line H and Line I form Group 1, and Line B is Group 2. Everything else is overlapping groups, with Line D being in Group 1 and Group 2, Line E in Group 0 and Group 1, and Line F and Line G are in all three of those groups. So there's two layers of grouping here, but I'm pretty sure there could be N depending on the complexity of the problem. And I'm also pretty sure there's a few catches to this that my example isn't representing.
What is the typical algorithm for handling this?