3

I've found a problem with the detection of angle types (whether inner or outer wrt the origin of axes), given a set of polylines. I've found dozens of very similar questions, but none of them solved my problem, so I put it here in hope something comes out.

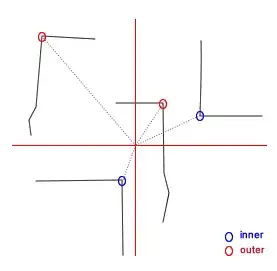
classification of angles

All I have is a set of polylines. I need to find the angles (with a given tolerance close to rectangles), and classify them as inner or outer.

For each polyline I take the vertices 3 by 3, and I am able to recognize whether the central one is or is not an angle, and measure its value as a number between 0 and 180 degrees.

Now I need to give this angle a direction (let's say a sign, negative if the acute is aiming away from the origin, positive if it aims toward the center), and I thought I'd implement it with one of the 2 methods below, but none of them worked.

1) Just the 'sign of a 2d crossproduct' (i know this is not mathematically correct terminology):

//given 3 contiguous vertices a,b,c
//check if b is a inner (+1) or outer (-1) vertex (0 in other cases)

double cross = ((b.x - a.x)*(c.y - a.y)) - ((b.y - a.y)*(c.x - a.x));

if(cross > 0){
  return 1;
} else if (cross < 0) {
  return -1;
}
return 0;

But it seems it only works in the bottom left quadrant, in the top right works exactly in the opposite way, while it screws in the others and i can't understand why.

2) Compare the norm of the vertices 

if b.norm() < a.norm() && b.norm() < c.norm 
then return +1
else return -1

This only works with basic cases, and overall no polylines crossing the axes (embracing the origin). I can check all the cases, but I'd rather avoid that.

Obviously, there are far safer methods, such as checking if the vertex is on the same side of the origin compared to a line passing between 2 neighbours lying on the 2 vectors.. but i need to optimize it as much as possible.

jalone
  • 1,953
  • 4
  • 27
  • 46
  • what are the values that you know and what is your starting point? – Ken Sep 12 '12 at 23:50
  • @Ken to simplify: i have 3 couple of double (each couple a point). thats should be enought, but i already have the smaller angle value between them and other elaboration, whose i eventually aggregate during optimization. – jalone Sep 12 '12 at 23:55
  • Is this a 2D or 3D problem? I don't know what you mean by "take vertices 3 by 3". But I only see x and y components mentioned in your question and a "2D cross product". – sellibitze Sep 13 '12 at 07:55
  • @sellibitze sorry maybe i was not clear enought, its a 2d problem. but a polyline is composed by N vertices, whose i take only 3 contiguous at a time to check if the middle one is outer or inner. – jalone Sep 13 '12 at 08:21

3 Answers3

4

The short version:

Describe the two angle vectors coming from the center point as a and b. And describe the vector from your center point to the origin as center.

The angle will be described as "inner" if:

dot( a + b, center ) > 0.0 && dot( cross( a, center ), cross( b, center ) ) < 0.0

The explanation:

This can be solved by using both the cross product and the dot product. (And happily, no angles at all. This can be solved entirely with adds, multiplies, and comparisons.)

Here it is, solved in two steps.

1. Is the angle pointing more toward the origin than away?

The angle is pointing more towards than away if you define the "direction the angle is pointing" by summing the two angle vectors.

Note that if the individual lengths of a and b are different, you can get some incorrect edge cases for very wide angles. Normalizing a and b will fix that.

`dot( a + b, center ) > 0.0`

2. Are vectors a and b pointing to opposite sides of the origin?

Vectors a and b are pointing to opposite sides of the origin if their cross products point in opposing directions.

`dot( cross( a, center ), cross( b, center ) ) < 0.0`

If and only if these are both true, your angle is defined as "inner".

Drew Dormann
  • 59,987
  • 13
  • 123
  • 180
  • i give it a try now, this would be perfect since i already have calculated all of these intermidiate values for other purposes. – jalone Sep 13 '12 at 06:24
  • @Drew Dormann a and b are vector from the origin (Oa, Ob) or from the center? (center-a , center-b)? i used the first case. being all 2d vectors, the result of crossProduct isn't a single value (representing the z-coord)? the dot product of two values is just their multiplication... this is how i did... and its NOT working :/ would you be so gentle to tell also why the following principle in the link (direction of the cross product) (as stated in my first attempt) is not good?: http://en.wikipedia.org/wiki/Graham_scan – jalone Sep 13 '12 at 15:42
  • @jalone In your diagram, you drew two solid lines and one dotted line for each example. Those three lines are `a`, `b`, and `center` in my answer. And they all start from the same point, for simplicity. The point you've circled. – Drew Dormann Sep 13 '12 at 16:49
  • 1
    @Drew Dormann Yes yes! I got it just while i was writing, thank you :) It works like a charm :) I unified this with other calculus and its really lightweight (i am in real time and huge amount of data) – jalone Sep 13 '12 at 18:10
3

To detect whether an angle abc is inner, you have to check whether the vector b0 (from b to origin) is a convex combination of vectors ba and bc.

If a vector px + qy is a convex combination of vectors p1x + q1y and p2x + q2y, there exists positive constants r and s such that r * (p1, q1) + s *(p2, q2) = (p, q). If we solve for r and s algebraically, we get r = (pq2 - p2q)/(p1q2 - q1p2) and s = (p1q - pq1)/(p1q2 - q1p2). If r and s are both positive, abc is inner.

krjampani
  • 2,902
  • 20
  • 23
0

Personally, I would just use the dot-product. Specifically (if a represents a vector from your vertex to the origin and b and c are your edge vectors pointing out of the vertex), then the angle is outer if both a dot b and a dot c are positive. Otherwise it's inner.

But i'm a bit confused about your real definition of 'inner' and 'outer'...

paddy
  • 60,864
  • 6
  • 61
  • 103
  • Ooops, i think i confused inner and outer. Corrected. I might still have misunderstood. – paddy Sep 13 '12 at 00:34
  • I think `a` and `b` can both point toward the origin, in the dot-product sense, but still not be "inner", as described here. Imagine a very narrow angle almost at a 90 degree angle to facing the origin. – Drew Dormann Sep 13 '12 at 00:43