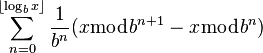Find the sum of digits of n+1,n+2.... when sum of digits of n is given

Question

We can easily compute the sum of digits of a given number but is there any mathematical formula or pattern we can use to determine the sum of next numbers without having to sum all the digits again and again?

For example

Sum of 1234 = 1+2+3+4 = 10
Sum of 1235 = 1+2+3+5 = 11
Sum of 1236 = 1+2+3+6 = 12

I can see some kind of pattern here but unable come up with any efficient math algorithm.

I use below method to calculate the sum of digits:

public int sum(long n) {  
    int sum = 0;   
    while (n != 0) {    
        sum += n % 10;
        n /= 10;  
    }  
    return sum;  
}

Which works fine but it is CPU intensive. I want to do this much faster. If I have a sequence of numbers, say 10->19 I should only have to count the digits for 10, then add one for each up to 19.

Is there any efficient way to calculate the sum of digits in numbers if I already have the sum of previous numbers?

Answer 1

DigitSum(n+1) = DigitSum(n) + 1 - (9 * NumberOfEndingZeros(n+1))

---

If you want to find not the digitsums of t consecutive numbers but the sum of the digitsums of t consecutive numbers (n+1, n+2, ..., n+t), it's simpler.

Sum(DigitSum(i)) for i = n+1 to n+t = a(n+t) - a(n)

where a(i) is the A037123 sequence from the Encyclopedia of Integer Sequences, which has several formulas. I think this will be quite fast:

a(n) = (1/2) * ( (n+1) * (n - 18 * sum{k>0, floor(n/10^k)} )
               + 9 * sum{k>0, (1+floor(n/10^k))*floor(n/10^k)*10^k}
               )

Answer 2

The fastest way would be to extract each digit and add it as you go.

public static void main(String... args) {
    // check values
    int runs = 1000000;
    for (int i = 100; i < runs; i++) {
        int sum = sumDigits(i - 1);
        int sum1 = sumDigits(i);
        int sum2 = sumDigits(sum, i);
        if (sum1 != sum2) throw new AssertionError(i + ": " + sum1 + " != " + sum2);
    }
    long start = System.nanoTime();
    for (int i = 0; i < runs; i++) {
        int sum = sumDigits(i);
        // prevent optimising away.
        if (sum < 0) throw new AssertionError();
    }
    long time = System.nanoTime() - start;
    System.out.printf("sumDigits took an average of %,d ns%n", time / runs);
    long start2 = System.nanoTime();
    int lastSum = 0;
    for (int i = 0; i < runs; i++) {
        int sum = sumDigits(lastSum, i);
        lastSum = sum;
        // prevent optimising away.
        if (sum < 0) throw new AssertionError();
    }
    long time2 = System.nanoTime() - start2;
    System.out.printf("sumDigits using previous value took an average of %,d ns%n", time2 / runs);

    long large = Long.MAX_VALUE - runs - 1;

    long start3 = System.nanoTime();
    for (int i = 0; i < runs; i++) {
        int sum = sumDigits(large + i);
        // prevent optimising away.
        if (sum < 0) throw new AssertionError();
    }
    long time3 = System.nanoTime() - start3;
    System.out.printf("sumDigits took an average of %,d ns%n", time3 / runs);
    long start4 = System.nanoTime();
    int lastSum2 = sumDigits(large);
    for (int i = 0; i < runs; i++) {
        int sum = sumDigits(lastSum2, large + i);
        lastSum2 = sum;
        // prevent optimising away.
        if (sum < 0) throw new AssertionError();
    }
    long time4 = System.nanoTime() - start4;
    System.out.printf("sumDigits using previous value took an average of %,d ns%n", time4 / runs);

}

public static int sumDigits(long n) {
    int sum = 0;
    do {
        sum += n % 10;
        n /= 10;
    } while (n > 0);
    return sum;
}

public static int sumDigits(int prevSum, long n) {
    while (n > 0 && n % 10 == 0) {
        prevSum -= 9;
        n /= 10;
    }
    return prevSum + 1;
}

prints

sumDigits took an average of 32 ns
sumDigits using previous value took an average of 10 ns
sumDigits took an average of 79 ns
sumDigits using previous value took an average of 7 ns

For large values, it can save around 70 ns. It add some complexity to your code. You have to use the first sumDigit to bootstrap the sum because you can't count all the way from 1 to 10^18.

Answer 3

Lets denote the sum of digits of a number n is s(n)

s(49) = 13

s(94) = 13

but 49+1 = 50 which s(50) = 5, while 94+1 = 95 which s(95) = 14. So if you were only given that the sum of digits of n is 13, you have at least two different possible answers for the sum of the digits of n+1. You need some additional information about n.

I do think a key is knowing that if n ends in a 9, s(n+1) will be at most s(n) - 9. (Ah, that's where ypercube's answer comes in.) So if you have xxxx9 (where the last x is anything but 9), s(xxxx9 + 1) = s(xxxx9) - 9 + 1. If you have xxx99, s(xxx99 + 1) = s(xxx99) - 18 + 1, etc.

So what might speed this up is if you count all the 10s, 100s, thousands, etc. in your range.

(Again, I see ypercube has beat me to the punch). It would appear that's what the formula for A037123 does exactly that (but from 0 to n). (Lets call that a(n))

So finally, since you're wanting the sum of the sum of digits from n to n+r, and not the sum from 1 to n, we need to see if we can derive a formula for sum of the sum of digits for a range ss(n,n+r)

That would appear to be simply

ss(n,n+r) = a(n+r) - a(n-1)

Answer 4

This is the formula from wikipedia:

This is my implementation in Java:

public static int digitSum(int x) {
    return IntStream.rangeClosed(0, (int) Math.log10(x)) // From zero to the number of digits of x in base 10...
               .map(n -> (x % (int) Math.pow(10, n + 1) -  x % (int) Math.pow(10, n)) / (int) Math.pow(10, n)) // ...yield each digit...
               .sum() // and sum;
}