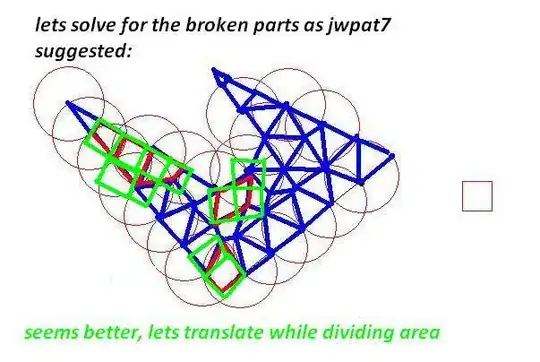
I've got some 2D polygons, each as a list of clockwise coordinates. The polygons are simple (i.e. they may be concave but they don't intersect themselves) and they don't overlap eachother.
I need to subdivide these polygons into smaller polygons to fit a size constraint. Just like the original polygons, the smaller ones should be simple (non-self-intersecting) and the constraint is they should each fit within one 'unit square' (which, for sake of simplicity, I can assume to be 1x1).
The thing is, I need to do this as efficiently as possible, where 'efficient' means the lowest number of resulting (small) polygons possible. Computation time is not important.
Is there some smart algorithm for this? At first I thought about recursively subdividing each polygon (splitting it in half, either horizontally or vertically whichever direction is larger) which works, but I don't seem to get very optimal results with this. Any ideas?