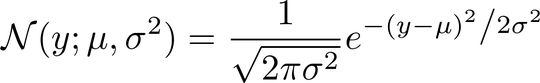In least-squares models, the cost function is defined as the square of the difference between the predicted value and the actual value as a function of the input.
When we do logistic regression, we change the cost function to be a logarithmic function instead of defining it to be the square of the difference between the sigmoid function (the output value) and the actual output.
Is it OK to change and define our own cost function to determine the parameters?
Yes, you can define your own loss function, but if you're a novice, you're probably better off using one from the literature. There are conditions that loss functions should meet:
They should approximate the actual loss you're trying to minimize. As was said in the other answer, the standard loss functions for classification is zero-one-loss (misclassification rate) and the ones used for training classifiers are approximations of that loss.
The squared-error loss from linear regression isn't used because it doesn't approximate zero-one-loss well: when your model predicts +50 for some sample while the intended answer was +1 (positive class), the prediction is on the correct side of the decision boundary so the zero-one-loss is zero, but the squared-error loss is still 49² = 2401. Some training algorithms will waste a lot of time getting predictions very close to {-1, +1} instead of focusing on getting just the sign/class label right.(*)
The loss function should work with your intended optimization algorithm. That's why zero-one-loss is not used directly: it doesn't work with gradient-based optimization methods since it doesn't have a well-defined gradient (or even a subgradient, like the hinge loss for SVMs has).
The main algorithm that optimizes the zero-one-loss directly is the old perceptron algorithm.
Also, when you plug in a custom loss function, you're no longer building a logistic regression model but some other kind of linear classifier.
(*) Squared error is used with linear discriminant analysis, but that's usually solved in close form instead of iteratively.
The logistic function, hinge-loss, smoothed hinge-loss, etc. are used because they are upper bounds on the zero-one binary classification loss.
These functions generally also penalize examples that are correctly classified but are still near the decision boundary, thus creating a "margin."
So, if you are doing binary classification, then you should certainly choose a standard loss function.
If you are trying to solve a different problem, then a different loss function will likely perform better.
The loss function is usually directly determined by the model when you fit your parameters using Maximum Likelihood Estimation (MLE), which is the most popular approach in Machine Learning.
You mentioned the Mean Squared Error as a loss function for linear regression. Then "we change the cost function to be a logarithmic function", referring to the Cross Entropy Loss. We didn't change the cost function. In fact, the Mean Squared Error is the Cross Entropy Loss for linear regression, when we assume yto be normally distributed by a Gaussian, whose mean is defined by Wx + b.
With MLE, you choose the parameters in way, that the likelihood of the training data is maximized. The likelihood of the whole training dataset is a product of the likelihoods of each training sample. Because that may underflow to zero, we usually maximize the log-likelihood of the training data / minimize the negative log-likelihood. Thus, the cost function becomes a sum of the negative log-likelihood of each training sample, which is given by:
-log(p(y | x; w))
where w are the parameters of our model (including the bias). Now, for logistic regression, that is the logarithm that you referred to. But what about the claim, that this also corresponds to the MSE for linear regression?
To show the MSE corresponds to the cross-entropy, we assume that y is normally distributed around a mean, which we predict using w^T x + b. We also assume that it has a fixed variance, so we don't predict the variance with our linear regression, only the mean of the Gaussian.
p(y | x; w) = N(y; w^T x + b, 1)
You can see, mean = w^T x + b and variance = 1
Now, the loss function corresponds to
-log N(y; w^T x + b, 1)
If we take a look at how the Gaussian N is defined, we see:
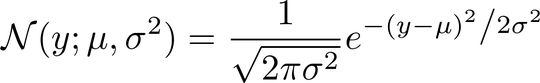
Now, take the negative logarithm of that. This results in:
We chose a fixed variance of 1. This makes the first term constant and reduces the second term to:
0.5 (y - mean)^2
Now, remember that we defined the mean as w^T x + b. Since the first term is constant, minimizing the negative logarithm of the Gaussian corresponds to minimizing
(y - w^T x + b)^2
which corresponds to minimizing the Mean Squared Error.
Yes, other cost functions can be used to determine the parameters.
The squared error function (commonly used function for linear regression) is not very suitable for logistic regression.
As in case of logistic regression the hypothesis is non-linear (sigmoid function), which makes the square error function to be non-convex.
The logarithmic function is a convex function for which there is no local optima, so gradient descent works well.
Assume that in your logistic regression model, you've scalar inputs x, and the the model outputs a probability $\hat{y}(x)=sigma(wx+b)$ for each input sample x .If you go ahead and build a quadratic loss function in the very special case where the inputs $x$ are scalars, then your cost function becomes: $C(w,b):= \Sigma_{x} | y(x) - \hat{y}(x)|^2=\Sigma_{x} | y(x) - \sigma(wx+b)|^2$. Now if you try to apply gradient descent on it, you'll see that: $C'(w), C'(b)$ are multiples of $\sigma'(wx+b)$. Now, sigmoid function being asymptotic, its derivative $\sigma'(z)$ becomes almost zero when the output $\sigma(z)$ is close to $0$ or $1$. This means: when the learning is bad, e.g. $\sigma(wx+b) \approx 0$, but $y(x)=1$, then $C'(w), C'(b)\approx 0$.
Now, the above situation is bad from two standpoints: (1) it makes gradient descent numerically much more expensive because even when we're far from minimizing C(w,b), we're not converging fast enough, and (2) it's counterintuitive to human learning: we learn fast when we make a big mistake.
However, if you calculate the C'(w) and C'(b) for cross-entropy cost function, this problem doesn't occur, as unlike the derivatives of quadratic cost, the derivatives of cross entropy cost is not a multiple of $sigma'(wx+b)$, and hence when the logistic regression model outputs close to 0 or 1, the gradient descent doesn't necessarily slow down, hence convergence to minima happens faster. You can find the relevant discussion here: http://neuralnetworksanddeeplearning.com/chap3.html, an excellent online book I highly recommend!
Besides, cross entropy cost functions are just negative log of maximum likelihood functions (MLE) used to estimate the model parameters, and in fact in the case of linear regression, minimizing the quadratic cost function is equivalent to maximizing the MLE, or equivalently, minimizing the negative log of MLE=cross entropy, with the underlying model assumption for linear regression-see P. 12 of http://cs229.stanford.edu/notes/cs229-notes1.pdf for more detail. Hence, for any machine learning model, be it classification and regression, finding the parameters by maximizing MLE (or minimizing cross entropy) has a statistical significance, whereas minimizing the quadratic cost for logistic regression doesn't have any (although it does for linear regression, as stated before).
I hope it clarifies things!
I'd like to say that the mathematics underlies mean square error is the Gaussian distribution of the error, while for logistic regression it is the distance of the two distributions: the underlying(ground truth) distribution and the predicted distribution.
How can we measure the distance between two distributions? In information theory, it is the relative entropy(also known as KL divergence), and the relative entropy is equivalent to the cross-entropy. And the logistic regression function is a special case of the softmax regression which is equivalent to cross-entropy and maximum entropy.
