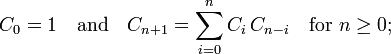How to find number of possible binary tree topological permutations?

Question

Given number of binary tree nodes (X) write method that returns the number of random permutations of binary trees with X nodes.

Examples:

X=1: 1

X=2: 2

     o    o
   o        o

X=3: 5

        o    o          o     o        o
      o        o      o         o    o   o
    o            o      o     o

I ended up with :

    public static int numOfPerms(int numOfNodes) {
       if (numOfNodes<=2 && numOfNodes > 0) {
           return numOfNodes;
       }
       int res = 1;
       for (int i=1; i<=numOfNodes; i++) {
           res = res*(4*i-1)/(i+1);
       }
       return res;
    }

I would appreciate sharing here better solutions.

you say 'permutations', but does the placement of each node in the tree matter? — Colin D, Jul 09 '12 at 14:55
so nodes are numbered and for example for case x=2 we have two simple trees: 1->2, 2->1? — Alexey A., Jul 09 '12 at 14:59
http://www.stringology.org/event/2009/psc09p17_presentation.pdf — Colin D, Jul 09 '12 at 14:59
@Alexey I think he just means the topology, the nodes themselve are the same (as showed in this examples). And the topology differs between left and right node. — brimborium, Jul 09 '12 at 15:00

Haile · Answer 1 · 2013-10-28T00:31:16.203

5

I think the Catalan Numbers can count your trees (See the part about applications in combinatorics). They form a well know sequence usually defined by this recurrence relations:

recurrence relation for C_n

This recurrence often arises in enumeration problems about tree or recursive structures, so it's quite well studied. The wikipedia entry I linked gives a number of useful closed-form expressions for the n-th Catalan number, i.e.

closed formulae

all of them are suitable for code implementation, and a lot faster than any recursive approach.

edited Oct 28 '13 at 00:31

answered Jul 09 '12 at 15:02

Haile

3,120
3
24
40

Yes, the [catalan numbers](http://oeis.org/A000108) match my own recursion: `f(0)=1; f(x)=sum(f(y)*f(x-y-1), y=0..(x-1))`. – MvG Jul 09 '12 at 15:14
You should post some actual information about catalan numbers and post the forumla for them. As per the faq, link only answers are frowned upon. – Colin D Jul 09 '12 at 15:18

brimborium · Answer 2 · 2012-07-09T15:38:02.127

4

Ok, as far as I can see, your solution is not correct, right? (for numOfNodes=4 it returns 12 instead of 14)

Intuitively, I would go for a recursive approach.

Use up one node as parent node
for all possible divisions into two sets, recursively call the function for both sets
multiply the results from the two sets of each division and sum up the products of all the divisions
return the sum

But before implementing it, I would make sure that there is no simple formula for this. I did not find one on the quick (which does not mean that there isn't one).

EDIT: As already stated in another answer: You could also just calculate the n-th Catalan number.

edited Jul 09 '12 at 15:38

answered Jul 09 '12 at 14:59

brimborium

9,362
9
48
76

The [Online Encyclopedia of Integer Sequences](http://oeis.org/) is always a good starting point when trying to turn a sequence into a formula. – MvG Jul 09 '12 at 15:16
Could you help me figure out why for `numOfNodes=4` answer should be 14 not 12? I'm counting it like this: `8` ways from lowest leafs (lets assume they are at level 4 of tree) to root (level 1) `+` `4` ways from leafs in level 3 to leafs at level 2. I don't count ways from lvl 2 to lvl 3 because they are the same as from lvl 3 to lvl 2. So it gives me 12... what am I missing? – Pshemo Jul 09 '12 at 15:46
@Pshemo in [this PDF](http://www.stringology.org/event/2009/psc09p17_presentation.pdf) that was linked by Colin D above, you can find all the permutations for 4 nodes on page 6. – brimborium Jul 09 '12 at 15:56
Thank you. Now I know I calculated wrong and not what I should :) – Pshemo Jul 09 '12 at 16:05
@Pshemo Yes, you missed the trees that have two leafs in level 3 (there are two of those trees) – brimborium Jul 09 '12 at 16:10
Not only that. I didn't know that same pattern can be counted only once. That task is tricky, I like it :) – Pshemo Jul 09 '12 at 16:13

score 2 · Accepted Answer · answered Jul 09 '12 at 15:40

Try this recursive method:

static int numOfPerms(int numOfNodes) {
    if (numOfNodes == 1) {
        return 1; 
    }

    numOfNodes = numOfNodes - 1;
    return ((numOfPerms(numOfNodes) * (2*numOfNodes+2) * 
            (2*numOfNodes+1))/((numOfNodes+1)*(numOfNodes+2)));
}

How to find number of possible binary tree topological permutations?

3 Answers3