9

how do I select a subset of points at a regular density? More formally,

Given

  1. a set A of irregularly spaced points,
  2. a metric of distance dist (e.g., Euclidean distance),
  3. and a target density d,

how can I select a smallest subset B that satisfies below?

  • for every point x in A,
  • there exists a point y in B
  • which satisfies dist(x,y) <= d

My current best shot is to

  • start with A itself
  • pick out the closest (or just particularly close) couple of points
  • randomly exclude one of them
  • repeat as long as the condition holds

and repeat the whole procedure for best luck. But are there better ways?

I'm trying to do this with 280,000 18-D points, but my question is in general strategy. So I also wish to know how to do it with 2-D points. And I don't really need a guarantee of a smallest subset. Any useful method is welcome. Thank you.

bottom-up method

  • select a random point
  • select among unselected y for which min(d(x,y) for x in selected) is largest
  • keep going!

I'll call it bottom-up and the one I originally posted top-down. This is much faster in the beginning, so for sparse sampling this should be better?

performance measure

If guarantee of optimality is not required, I think these two indicators could be useful:

  • radius of coverage: max {y in unselected} min(d(x,y) for x in selected)
  • radius of economy: min {y in selected != x} min(d(x,y) for x in selected)

RC is minimum allowed d, and there is no absolute inequality between these two. But RC <= RE is more desirable.

my little methods

For a little demonstration of that "performance measure," I generated 256 2-D points distributed uniformly or by standard normal distribution. Then I tried my top-down and bottom-up methods with them. And this is what I got:

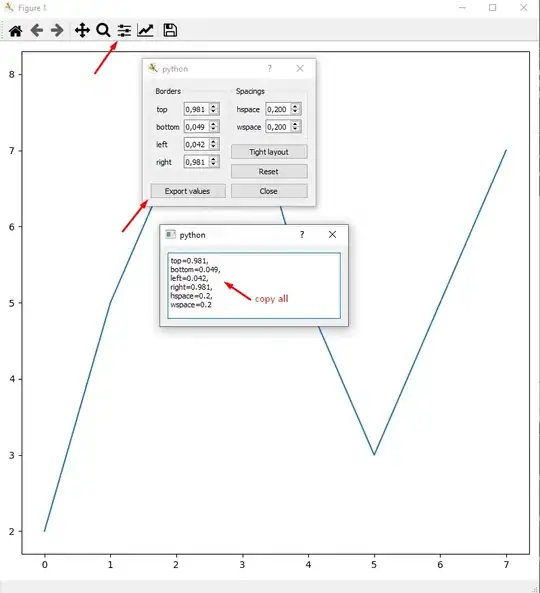
bottom-up.norm top-down.norm

RC is red, RE is blue. X axis is number of selected points. Did you think bottom-up could be as good? I thought so watching the animation, but it seems top-down is significantly better (look at the sparse region). Nevertheless, not too horrible given that it's much faster.

Here I packed everything.

http://www.filehosting.org/file/details/352267/density_sampling.tar.gz

h2kyeong
  • 447
  • 3
  • 13
  • I can't see how your methods satisfy the condition stated (`for every x in A there is an y in B such that dist(x, y) < d`) on the code you have provided. I am unable to find the python `h2` package you are using either. – salva Jun 18 '12 at 07:09
  • My little method does it backwards -- it creates selections that are effective for _some_ **d**. And sorry, ``h2`` is my collection reusable chunks of code... I wasn't aware that I used it. – h2kyeong Jul 02 '12 at 14:22

4 Answers4

3

You can model your problem with graphs, assume points as nodes, and connect two nodes with edge if their distance is smaller than d, Now you should find the minimum number of vertex such that they are with their connected vertices cover all nodes of graph, this is minimum vertex cover problem (which is NP-Hard in general), but you can use fast 2-approximation : repeatedly taking both endpoints of an edge into the vertex cover, then removing them from the graph.

P.S: sure you should select nodes which are fully disconnected from the graph, After removing this nodes (means selecting them), your problem is vertex cover.

Saeed Amiri
  • 22,252
  • 5
  • 45
  • 83
  • Yes, this problem falls into set cover. But in this problem we have the general property that if A and B are close and B and C are close then A and C tend to be close. That's why I think there could be a better way. Thanks. – h2kyeong Jun 11 '12 at 08:45
  • @h2kyeong, how you have this property?"if A and B are close and B and C are close then A and C tend to be close"? assume A and B and C are on straight line (first A, second B, after that C), and `||A-B||=d, ||B-C||=d, but ||A-C|| = 2d`. So you can't assume you have this property except you mention it in your question explicitly and in this case problem is too easy. – Saeed Amiri Jun 11 '12 at 09:10
  • yes, for instance with Euclidean distance, the upper limit is 2 **d** and lower limit is zero. I wan't saying it is limited to **d**; but 2 **d** is still proportionally small. Meanwhile, the distance function may assign arbitrary values to all point pairs and still it will be a subproblem of vertex cover. – h2kyeong Jun 11 '12 at 11:36
  • @h2kyeong, I can't understand what you mean, if you set limit as **d** how you say **2d** is OK? – Saeed Amiri Jun 11 '12 at 20:45
  • I was just saying that many distance functions are far from random. So we have more hope for a faster solution than those for vertex cover. Sadly I learned that even picking out the closest pair isn't so easy in high dimensions... – h2kyeong Jun 12 '12 at 05:54
2

A genetic algorithm may probably produce good results here.

update:

I have been playing a little with this problem and these are my findings:

A simple method (call it random-selection) to obtain a set of points fulfilling the stated condition is as follows:

  1. start with B empty
  2. select a random point x from A and place it in B
  3. remove from A every point y such that dist(x, y) < d
  4. while A is not empty go to 2

A kd-tree can be used to perform the look ups in step 3 relatively fast.

The experiments I have run in 2D show that the subsets generated are approximately half the size of the ones generated by your top-down approach.

Then I have used this random-selection algorithm to seed a genetic algorithm that resulted in a further 25% reduction on the size of the subsets.

For mutation, giving a chromosome representing a subset B, I randomly choose an hyperball inside the minimal axis-aligned hyperbox that covers all the points in A. Then, I remove from B all the points that are also in the hyperball and use the random-selection to complete it again.

For crossover I employ a similar approach, using a random hyperball to divide the mother and father chromosomes.

I have implemented everything in Perl using my wrapper for the GAUL library (GAUL can be obtained from here.

The script is here: https://github.com/salva/p5-AI-GAUL/blob/master/examples/point_density.pl

It accepts a list of n-dimensional points from stdin and generates a collection of pictures showing the best solution for every iteration of the genetic algorithm. The companion script https://github.com/salva/p5-AI-GAUL/blob/master/examples/point_gen.pl can be used to generate the random points with a uniform distribution.

salva
  • 9,943
  • 4
  • 29
  • 57
  • Could you elaborate a bit more about this? Of course, when knowing nothing about the problem domain, throwing a genetic algorithm at it is always an option. – Christian Rau Jun 13 '12 at 15:09
  • @Christian, yes, you can use bitmaps to represent the covering subsets. As weighting function you can use the bit count (number of points in the covering subset), and for breeding, for instance, you can mix two bitmaps selecting substrings for both randomly and them repairing them to ensure they are covering subsets. – salva Jun 13 '12 at 15:29
  • @Christian, actually, I am trying to code a full solution :-) – salva Jun 13 '12 at 16:31
  • so you see it as set cover problem. I hope you find good breeding / mutating methods... especially breeding. – h2kyeong Jun 14 '12 at 04:27
2

Here is a proposal which makes an assumption of Manhattan distance metric:

  1. Divide up the entire space into a grid of granularity d. Formally: partition A so that points (x1,...,xn) and (y1,...,yn) are in the same partition exactly when (floor(x1/d),...,floor(xn/d))=(floor(y1/d),...,floor(yn/d)).
  2. Pick one point (arbitrarily) from each grid space -- that is, choose a representative from each set in the partition created in step 1. Don't worry if some grid spaces are empty! Simply don't choose a representative for this space.

Actually, the implementation won't have to do any real work to do step one, and step two can be done in one pass through the points, using a hash of the partition identifier (the (floor(x1/d),...,floor(xn/d))) to check whether we have already chosen a representative for a particular grid space, so this can be very, very fast.

Some other distance metrics may be able to use an adapted approach. For example, the Euclidean metric could use d/sqrt(n)-size grids. In this case, you might want to add a post-processing step that tries to reduce the cover a bit (since the grids described above are no longer exactly radius-d balls -- the balls overlap neighboring grids a bit), but I'm not sure how that part would look.

Daniel Wagner
  • 145,880
  • 9
  • 220
  • 380
  • A simple improvement to this approach is to use a triangular grid instead of a square one. This way, there is less overlap between the balls. – salva Jun 21 '12 at 09:04
  • 1
    @salva Well, that may be better for a 2D Euclidean metric, though hexagons would be even better for that. But the OP seems to want a higher-dimensional thing -- do you happen to know off-hand what the 18-dimensional tiling shapes are? =) – Daniel Wagner Jun 21 '12 at 10:10
  • a hexagonal grid and a triangular grid are two views of the same geometric structure. Just draw a hexagonal grid and then join the centers of contiguous hexagons to find its triangular equivalent. Regarding higher dimensions, the triangle/tetrahedron generalization is the [simplex](http://en.wikipedia.org/wiki/Simplex). – salva Jun 21 '12 at 10:43
0

To be lazy, this can be casted to a set cover problem, which can be handled by mixed-integer problem solver/optimizers. Here is a GNU MathProg model for the GLPK LP/MIP solver. Here C denotes which point can "satisfy" each point.

param N, integer, > 0;
set C{1..N};

var x{i in 1..N}, binary;
s.t. cover{i in 1..N}: sum{j in C[i]} x[j] >= 1;
minimize goal: sum{i in 1..N} x[i];

With normally distributed 1000 points, it didn't find the optimum subset in 4 minutes, but it said it knew the true minimum and it selected only one more point.

h2kyeong
  • 447
  • 3
  • 13