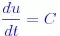2D Projectile tracing path clarification

Question

Projectile tracing path Problem in 2D game:

Assumption:

We make the simplifying assumption that gravity is constant and that there is no wind or drag. The motion of the projectile is given by the following equations:

x = x0 + v0t cos(theta)

y = y0 + v0t sin(theta) + .5 g t^2

where (x0, y0) is the initial position, v0 the initial velocity (magnitude only), theta the angle of discharge, and g the gravitational acceleration. Solving the first equation for v0t and substituting into the second, we get equation [1]:

y = y0 + (x-x0) tan(theta) + .5 (g/v0^2) (x-x0)^2 / cos(theta)^2

Calibration:

Calibration is the process of determining the value of g from an actual projectile. To do that, we shoot a random projectile and capture:

1. The starting point (x0, y0)
2. The aim vector (v0, theta)
3. A random point on the curve (x1, y1)

Substituting the values into the equation [1] and solving for g, we get:

g = (v0^2) * {[2 cos(theta)^2 (y1-y0) / (x1-x0)^2] - [sin(2theta) / (x1-x0)]}

Application:

Now that we have g, we can substitute it back into equation [1], which now can be used to trace the path of a projectile from any starting point and initial velocity. (this is the part I don’t understand)

g=5.89

(x0,y0) starting position = 0,0

Initial velocity = 1-100

Discharge Angle = 0-360

can someone please explain how to get the full plotted path of the parabola for any initial velocity between 1-100, and for any discharge angle between 0-360, if the acceleration due to gravity is 5.89 (in this game), and the starting position is 0,0?

I am a complete newb at math, all of this stuff not in bold lettering I found elsewhere and have been racking my brain over. Please assume I know nothing.

Answer 1

You only miss the time t in your first set of equations and the spacial/time constrain, plot the first x second of the projectile or until the projectile left the bounding box m. so the pseudocode would be:

• t=0; x(0)=some coordinate; y(0)=another coordinate
• LOOP t
• t=t+1
• Calculate coordinates {X(t=1), Y(t=1)}
• Draw the point or the line between this point an the previous one
• LOOP UNTIL t>time limit OR point {X(t), Y(t)} is outside your bounding box

I hope this help in your endevour

Answer 2

Choosing v0 = 10 and theta = 60 degrees we have

tan(theta) = 1.732
cos(theta) = 0.5

and thus equation 1 reads (x0=0, y0=0, g=5.89 were given)

y = 1.732*x - 0.1178*x^2

which can be plotted directly (y vs. x): see here

Note: I corrected the - sign for gravity.

Answer 3

It's a pretty simple undergraduate physics problem. You start with Newton's law for the x- and y-directions:

with initial conditions:

Where Q is the initial speed of the projectile and theta is the angle measured counterclockwise from the horizon if the gun points to the right.

So if you integrate each one once w.r.t. time, you get:

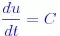
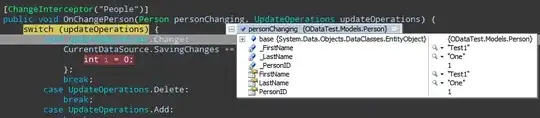
Applying initial conditions:

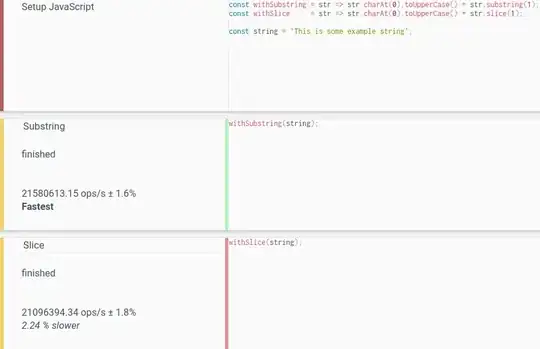
Integrating a second time gives:

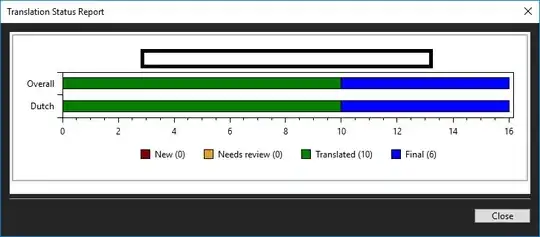
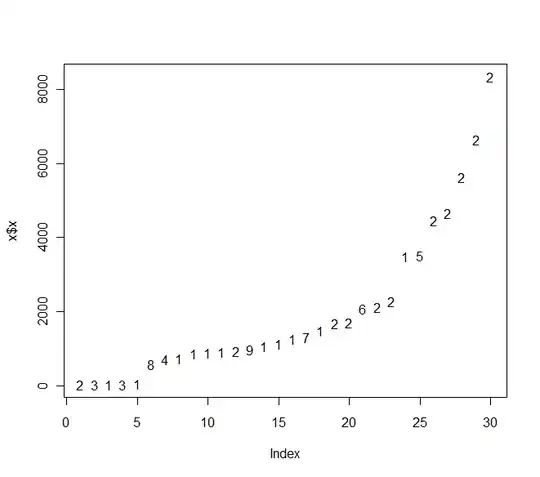
Applying initial conditions again:

Making the substitutions gives the final equations that you want for the (u, v) position of the projectile from the moment the gun goes off:

If you put the origin of the coordinate system at the gun muzzle exit, then the two initial displacements are zero.

Now you have two equations for the (u, v) position of the projectile. You can plug in the initial speed of the projectile and the angle of the gun as measured from the horizon at zero, pointing to the right.

You just start with time at zero, pick an increment in time, and loop for as long a time interval as you like. You plug the current value of time into those equations, evaluate the results, increment the time, and repeat.

Let's imagine that you angle the gun at forty-five degrees counterclockwise from the horizon and fire a projectile at 1000 in/sec. You can step through time and see the projectile move up and to the right in a parabolic path until it reaches its apex and then starts to fall back to the horizon. Eventually your y-displacement will return back to zero and then continue into negative territory, as if you had shot it from the edge of a cliff.

If you want to know how far the projectile goes before it hits the ground, just stop the time loop when the height becomes less than or equal to zero:

Here's a Java implementation for you:

package physics;

/**
 * CannonSimulator simulates shooting a projectile.  Users are responsible for making
 * sure that all constants use consistent units (e.g. meters for length, seconds for
 * time, kg for mass, etc.)
 * @author Michael
 * @since 6/14/12 9:47 PM
 * @link http://stackoverflow.com/questions/10935060/2d-projectile-tracing-path-clarification/11043389#11043389
 */
public class CannonSimulator {

    private double m;
    private double g;
    private double q;
    private double theta;

    public static void main(String[] args) {
        double m = ((args.length > 0) ? Double.valueOf(args[0]) : 1.0); // default mass is 1 kg
        double g = ((args.length > 1) ? Double.valueOf(args[1]) : 9.8); // default gravity is 9.8 m/sec^2
        double q = ((args.length > 2) ? Double.valueOf(args[2]) : 100.0); // default velocity is 100 m/sec
        double theta = ((args.length > 3 ? Double.valueOf(args[3]) : Math.PI/4.0)); // default angle is 45 degrees
        CannonSimulator simulator = new CannonSimulator(m, g, q, theta);
        double t = 0.0;
        double dt = 0.001; // time increment of 0.1 seconds
        while (simulator.v(t) >= 0.0) {
            System.out.println(String.format("time: %10.3f u: %10.3f v: %10.3f", t, simulator.u(t), simulator.v(t)));
            t += dt;
        }
    }

    public CannonSimulator(double m, double g, double q, double theta) {
        if (m <= 0.0) throw new IllegalArgumentException("mass must be greater than zero");
        if (g <= 0.0) throw new IllegalArgumentException("gravity must be greater than zero");
        if (q <= 0.0) throw new IllegalArgumentException("velocity must be greater than zero");

        this.m = m;
        this.g = g;
        this.q = q;
        this.theta = theta;
    }

    public double v(double time) {
        return time*(q*Math.sin(theta) - g*time/m);
    }

    public double u(double time) {
        return time*q*Math.cos(theta);
    }
}

That's how to solve this problem.