On Diffie-Hellman key exchange

Question

The book I am reading, explains the algorithm as follows:

• 2 people think of 2 public "n and g" numbers both are aware of.
• 2 people think of 2 private "x and "y" numbers they keep secret.

Exchange happens as illustrated

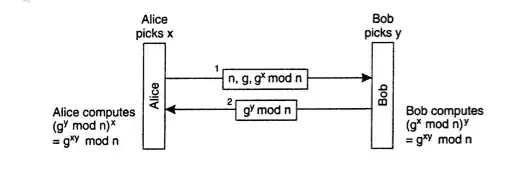
I put together the following python code to see how this works and .... it does not. Please help me understand what am i missing:

 #!/usr/bin/python

 n=22 # publicly known 
 g=42 # publicly known

 x=13 # only Alice knows this 
 y=53 # only Bob knows this

 aliceSends = (g**x)%n 
 bobComputes = aliceSends**y 
 bobSends = (g**y)%n
 aliceComputes = bobSends**x


 print "Alice sends    ", aliceSends 
 print "Bob computes   ", bobComputes 
 print "Bob sends      ", bobSends 
 print "Alice computes ", aliceComputes

 print "In theory both should have ", (g**(x*y))%n

 ---

 Alice sends     14  
 Bob computes    5556302616191343498765890791686005349041729624255239232159744 
 Bob sends       14 
 Alice computes  793714773254144 

 In theory both should have  16

Answer 1

You forgot two more modulos:

>>> 5556302616191343498765890791686005349041729624255239232159744 % 22
16L
>>> 793714773254144 % 22
16

Answer 2

Roman is right. However, you'd better have a look at pow() three arguments function. Much faster and third argument is modulus

Answer 3

For two people

#!/usr/bin/python
p=141301# publicly known 
g=5728435 # publicly known
x=76435 # only Alice knows this 
y=37846 # only Bob knows this
aliceSends = (g**x)%p 
aliceComputes = (bobSends**x)%p
bobSends = (g**y)%p
bobComputes = (aliceSends**y) %p
bobSends = (g**y)%p
bobComputes = (aliceSends**y) %p
print ("Alice sends    ", aliceSends )
print ("Bob computes   ", bobComputes )
print ("Bob sends      ", bobSends)
print ("Alice computes ", aliceComputes)

For three or more people

#!/usr/bin/python
p=141301# publicly known 
g=5728435 # publicly known
x=76435 # only Alice knows this 
y=37846 # only Bob knows this
z=23# only carol knows this
aliceSends = (g**x)%p 
bobSends = (aliceSends**y)%p
carolComputes=(bobSends**z)%p
bobSends2=(g**y)%p
carolSends=(bobSends2**z)%p
aliceComputes=(carolSends**x)%p
carolSends2=(g**z)%p
aliceSends2=(carolSends2**x)%p
bobComputes=(aliceSends2**y)%p
print ("Alice computes ga and sends it to Bob.",aliceSends)
print ("Bob computes (ga)b = gab and sends it to Carol.",bobSends)
print ("Carol computes (gab)c = gabc and uses it as her secret.",carolComputes)
print ("Bob computes gb and sends it to Carol.",bobSends2)
print ("Carol computes (gb)c = gbc and sends it to Alice.",carolSends)
print ("Alice computes (gbc)a = gbca = gabc and uses it as her  secret.",aliceComputes)
print ("Carol computes gc and sends it to Alice.",carolSends2)
print ("Alice computes (gc)a = gca and sends it to Bob.",aliceSends2)
print ("Bob computes (gca)b = gcab = gabc and uses it as his 
secret.",bobComputes)