I can not understand how splaying works.
The part that I can not follow is how we know if a: i) zig ii) zig-zag or iii) zig-zig must be done.
If I understand correctly this has to do with the current node in the path.
If it is the root's child then it is a zig otherwise either (ii) or (iii) depending on if the parent of current node and current node are both left (or right) children. Ok so far.
Now the part I don't get:
As we move down isn't the process to "remove" the intermediate nodes into left and right subtrees so that we have a middle tree that will be eventually the root of the item under search?
Then if we start from a tree we would be doing continually zig and nothing else since we are removing elements and are always at the root.
Example:
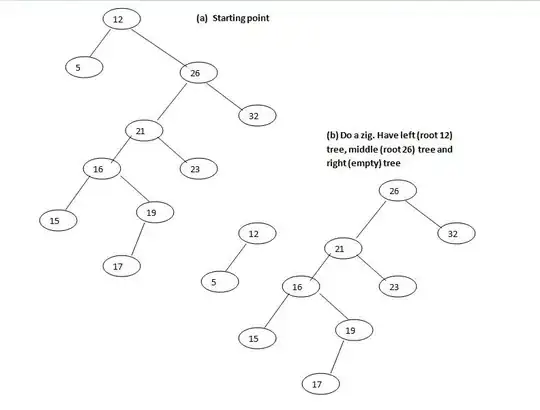
If for example I am looking for 20 I would start at the root and go left. So the current node has root as parent and I do a zig. Now what happens?? I am at 26 and go left but isn't 26 also root? So should I be doing a zig?
But from what I see in this example a zig-zag is being done and I can not understand why.
Any help here?
- 52,998
- 69
- 209
- 339
-
I haven't looked at [splay trees](http://en.wikipedia.org/wiki/Splay_tree) in a while, but I'm pretty sure that's not even remotely how they work. – Mooing Duck May 29 '12 at 22:31
-
@MooingDuck:Ok......So now how am I helped with this comment?If you have some link that you think could help me clear this out please post it. – Cratylus May 30 '12 at 15:19
-
it's hard to see on this site, but the words "splay trees" in my previous comment _was_ a link :P – Mooing Duck May 30 '12 at 15:30
1 Answers
By root they mean root of the entire tree, not root of the subtree you are splaying. So, in your example 12 is the root of the entire tree.
...
If you'd like an example to work from, I coded up a SplayTree in Java recently. You can find the code here.
The big thing with splay tree's is they move the most recently inserted/queried node up (at most) two levels in the tree. You have to perform a zig, zig-zig, or zig-zag based on it's grand parent and parent node locations.
When a node x is accessed, a splay operation is performed on x to move it to the root. To perform a splay operation we carry out a sequence of splay steps, each of which moves x closer to the root.
The three types of splay steps are: (g = grand parent, p = parent, and x = node to splay)
- Zig Step: This step is done when p is the root. The tree is rotated on the edge between x and p.
- Zig-zig Step: This step is done when p is not the root and x and p are either both right children or are both left children. The tree is rotated on the edge joining p with its parent g, then rotated on the edge joining x with p.
- Zig-zag Step: This step is done when p is not the root and x is a right child and p is a left child or vice versa. The tree is rotated on the edge between x and p, then rotated on the edge between x and its new parent g.
http://en.wikipedia.org/wiki/Splay_tree
Below is splaying of node 3 in the tree.
Tree before splaying:
└── 0
└── (right) 9
└── (left) 7
├── (left) 5
│ ├── (left) 1
│ │ └── (right) 2
│ │ └── (right) 4
│ │ └── (left) 3
│ └── (right) 6
└── (right) 8
After a (right->left) Zig-Zag to node 3.
└── 0
└── (right) 9
└── (left) 7
├── (left) 5
│ ├── (left) 1
│ │ └── (right) 3
│ │ ├── (left) 2
│ │ └── (right) 4
│ └── (right) 6
└── (right) 8
After another (left->right) Zig-Zag to node 3.
└── 0
└── (right) 9
└── (left) 7
├── (left) 3
│ ├── (left) 1
│ │ └── (right) 2
│ └── (right) 5
│ ├── (left) 4
│ └── (right) 6
└── (right) 8
After a (left->left) Zig-Zig to node 3.
└── 0
└── (right) 3
├── (left) 1
│ └── (right) 2
└── (right) 7
├── (left) 5
│ ├── (left) 4
│ └── (right) 6
└── (right) 9
└── (left) 8
After a (right) Zig to node 3. Now time to stop since 3 is in the root position.
└── 3
├── (left) 0
│ └── (right) 1
│ └── (right) 2
└── (right) 7
├── (left) 5
│ ├── (left) 4
│ └── (right) 6
└── (right) 9
└── (left) 8t) 6
└── (right) 9
└── (left) 8
If you try and access node 3 again in the Tree, it would not have to be splayed since it's already in the root position.
- 4,196
- 4
- 24
- 48
-
I don't understand your example: 1)`You see, it moved 15 up two levels with a rotation` there is no 15 in your tree 2)`splaying the node with value of 7` what does this mean?That we search for 7? Why isn't 7 the root of the whole tree now? – Cratylus May 30 '12 at 15:59
-
-
Splaying doesn't make the node the root of the entire tree, it just moves the root up at most two levels in the tree. If you splay the same node multiple times, it'll eventually end up in the root. Basically, splaying will move the node into it's grandparent's position in the tree. – Justin May 30 '12 at 16:14
-
splaying occurs after insertion/searching/deleting of nodes in a Splay Tree. With the exception that you actually splay the node's parent when deleting a node. – Justin May 30 '12 at 16:15
-
What you are saying is not consistent with what I have been reading. E.g.`When a node x is accessed, a splay operation is performed on x to move it to the root` from wiki.I have been reading that the item under "access" always goes to the root. Not to the gradparent – Cratylus May 30 '12 at 16:33
-
Wikipedia is inconsistent. The same sentence you just posted from Wikipedia. "When a node x is accessed, a splay operation is performed on x to move it to the root. To perform a splay operation we carry out a sequence of splay steps, each of which moves x closer to the root." All the diagrams are correct on wikipedia which show an access moves a node to the parent position, if the parent is root , else to the granparent. – Justin May 30 '12 at 16:35
-
From what I have been reading the benefit/usage of the splay trees is that when a node is accessed it is placed to the root.As a result operations for same items are really fast. What you are saying is that it just moves the node up 2 levels? But this does not give the performance benefits advertised for splay trees – Cratylus May 30 '12 at 16:52
-
Even if a splayed node should be in the root position after splaying. It's not a single splay that'll do it. You'd repeatably have to splay the node until it reaches the the root position using the three types of splay operations which moves the node up at most two levels per operation. – Justin May 30 '12 at 16:53
-
One benefit of a splay tree is fast access to nodes which you access often. But the other benefit is it somewhat balances the tree during the splaying process. – Justin May 30 '12 at 17:00
-
`repeatably have to splay the node ` Yes, this is my OP. I can't follow how to decide between zig/zig-zig/zig-zag if current item is always the root – Cratylus May 30 '12 at 17:14
-
If the current item is the root, you don't have to splay it. I'm adjusting my answer, to try and help. – Justin May 30 '12 at 17:19
-
It helps.I tried to do an implementation of this.If you could please give it a look (I posted only splay and find) and tell me what you think it would be great. In here: http://codereview.stackexchange.com/questions/12195/please-review-my-implementation-of-splay-tree – Cratylus May 31 '12 at 16:17
-
I can only speak to the logic of your code since I can't see the whole class but it looks correct to me. The only thing I noticed is it isn't thread safe but that's the least of your worries. – Justin May 31 '12 at 21:50
-