9

I am looking for an implementation of bidirectional search (a.k.a. "meet in the middle" algorithm) for Dijkstra (or any other source-to-destination shortest path algorithm) in Java.

As bidirectional search processing is trickier than it looks like (Graph Algorithms, p.26), I want to consider an existing implementation before reinventing the wheel!

P.S.: I am talking about bidirectional search, not to be confused with a bidirectional graph)

Here is an example of a tricky graph:

enter image description here

Nayuki
  • 17,911
  • 6
  • 53
  • 80
Fabien
  • 965
  • 3
  • 11
  • 23
  • My implementation for bi-directional graph is exactly the same as in the directed case - I simply add two edges instead of one. I don't know why do you think it is harder. – Ivaylo Strandjev May 28 '12 at 11:16
  • Bidirectional dijkstra means that dijkstra is processed in parallel both from source and destination, reducing complexity cost. See http://en.wikipedia.org/w/index.php?title=Bidirectional_search – Fabien May 28 '12 at 12:00
  • I'm not seeing how this algorithm is significantly harder than a normal Dijkstra implementation. (In any event, implementations will be very different depending on how the graph is provided, so any implementation someone else provided will probably require rewriting anyway.) – Louis Wasserman May 28 '12 at 12:03
  • @Fabien, ah, sorry I could not open the first article. I know this approach by the name "meet in the middle". It is a bit harder then the original Dijkstra but not that much. Maybe mention the parts that are hard for you? – Ivaylo Strandjev May 28 '12 at 12:22
  • 3
    I think that it may be unclear when to stop searching, because if we stop immediately after the meeting, it will not guarantee that the path is the shortest. And stopping too late results in a slow algorithm. – fdermishin May 28 '12 at 12:33
  • Here is an implementation, but it is in C#, not Java and it seems that the resulting path is not always optimal. – fdermishin May 28 '12 at 12:52
  • 1
    a bit late ... but have a look into https://github.com/graphhopper/graphhopper/ – Karussell Sep 29 '12 at 10:44
  • 2
    @user502144 nailed it. The stopping condition is not immediately obvious, but there is one. See http://www.cs.princeton.edu/courses/archive/spr06/cos423/Handouts/EPP%20shortest%20path%20algorithms.pdf – Erick G. Hagstrom Mar 03 '16 at 15:10
  • Possible duplicate of ["Bidirectional Dijkstra" by NetworkX](http://stackoverflow.com/questions/35779969/bidirectional-dijkstra-by-networkx) – Joel Mar 03 '16 at 23:59

1 Answers1

8

Yes, there is at least in Java: https://github.com/coderodde/GraphSearchPal/blob/master/src/main/java/net/coderodde/gsp/model/support/BidirectionalDijkstraPathFinder.java

In a bidirectional Dijkstra's algorithm, you maintain actually two "Dijkstra's algorithms": the forward search and the backward search. Now, the forward search resembles a lot the unidirectional Dijkstra's algorithm. The backward search, however, proceeds in "reversed" fashion. If there is a directed edge (colloquially called an arc) (u, v), the forward search would traverse it from u to v, whereas the backward search would do the same in opposite direction.

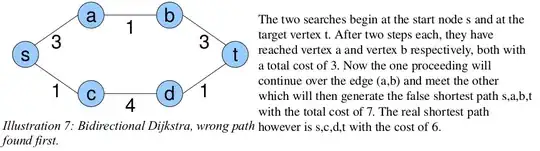
Because the two search processes meet (usually) somewhere in between the source node and the target node, we need another termination condition, which in bidirectional Dijkstra's algorithm is 

g(top(OPEN_forward)) + g(top(OPEN_backward)) > l

where l is the length of the shortest known so far path between the source and target nodes.

Additional code you might see only in bidirectional version is checking the possibility of shortening a shortest path candidate every time you improve the g value of any node. (The g value of a node u is the shortest (known so far) distance from the node from which the search started to u.)

coderodde
  • 1,269
  • 4
  • 17
  • 34