How to differentiate between a double peak and a single peak array?
Also if the array represents a double peak, how to find the minimum point between two peaks? The minimum points outside of the peaks (left of left peak and right of right peak) should not be considered in finding the minimum point.
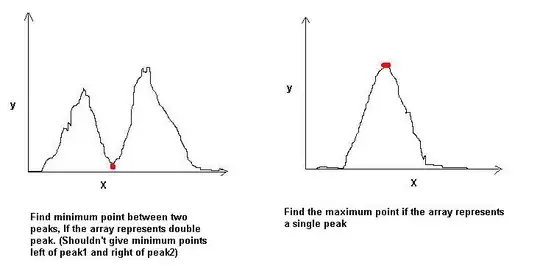
Here is one algorithm that might work depending on how noisy your signal is. Here I define a peak as the set of connected points greater than a given threshold value.
Assuming your original data is in the array A. First, find a threshold:
t = (max(A)+min(A))/2;
Next, find all the points greater than this threshold t:
P = A>t;
Count number of connected entries points that are greater than t using bwlabel
L = bwlabel(P);
numberOfPeaks = max(L);
Now numberOfPeaks should tell you how many peaks (connected points greater than the threshold value) you have in your data
Now to find the minimum point between the two peak we need to identify those points that seperate the two peaks using the label matrix L.
firstPoint = find(L==1,1,'last')+1;
lastPoint = find(L==2,1,'first')-1;
So the valley between the first two peaks is the points with index between firsPoint and lastPoint. The minimum would then be
minValue = min(A(firstPoint:lastPoint));
Solution that does not depend on the Image Processing Toolbox
As @Nzbuu notes the aboth relies on the image processing toolbox function bwlabel. So, here is away to avoid that. First, I Assume that the the array P correctly identifies points belonging to peak (P(i)=1) and those belonging to valleys (P(i)=-1). If this is the case the boundary between peaks and valleys can be identified when dP = P(i+1)-P(i) = 1 or -1.
dP = diff(P);
To calculate the number of peaks simply sum the number of 1's in dP:
numberOfPeaks = sum(dP==1);
And the points identifying the first valley are between
firstPoint = find(dP==-1,1,'first')+1 %# the -1 represents the last point of the peak so add 1
lastPoint = find(dP==1,2,'first'); #% Find the start of the second peak
lastPoint = lastPoint(end); #% Keep the last value
I found PEAKDET function to be quite reliable and fast although it's loop based. It does not require pre-smoothing of noisy data, but finds local max and min extrema with difference larger than parameter delta.
Since PEAKDET runs from left to right it sometime misses peaks on the right site. To avoid it I prefer to run it twice:
%# some data
n = 100;
x = linspace(0,3*pi,n);
y = sin(x) + rand(1,n)/5;
%# run peakdet twice left-to-right and right-to-left
delta = 0.5;
[ymaxtab, ymintab] = peakdet(y, delta, x);
[ymaxtab2, ymintab2] = peakdet(y(end:-1:1), delta, x(end:-1:1));
ymaxtab = unique([ymaxtab; ymaxtab2],'rows');
ymintab = unique([ymintab; ymintab2],'rows');
%# plot the curve and show extreme points based on number of peaks
plot(x,y)
hold on
if size(ymaxtab,1) == 2 && size(ymintab,1) == 1 %# if double peak
plot(ymintab(:,1),ymintab(:,2),'r.','markersize',30)
elseif size(ymaxtab,1) == 1 && size(ymintab,1) == 0 %# if single peak
plot(ymaxtab(:,1),ymaxtab(:,2),'r.','markersize',30)
else %# if more (or less)
plot(ymintab(:,1),ymintab(:,2),'r.','markersize',30)
plot(ymaxtab(:,1),ymaxtab(:,2),'r.','markersize',30)
end
hold off
You can find the local min/max as follows:
x = 0:.1:4*pi;
y = sin(x);
plot(x,y)
diffy = diff(y);
localMin = find(diffy(1:end-1)<=0 & diffy(2:end) > 0)+1;
localMax = find(diffy(1:end-1)>=0 & diffy(2:end) < 0)+1;
hold on
plot(x(localMin),y(localMin),'dg')
plot(x(localMax),y(localMax),'*r')
Resulting in:
Basically you are finding where the delta between the y values change signs. If your data is noisy this will cause lots of local min/max values and you may need to filter your data.
To find the minimum value between two peaks you can do something like this:
if numel(localMax) == 1
fprintf('The max value is: %f',y(localMax));
elseif numel(localMax > 1)
betweenPeaksIndex = localMin(localMin > localMax(1) & localMin <localMax(2));
fprintf('The min between the first 2 peaks is: %f',y(betweenPeaksIndex));
else
fprintf('The was no local Max ..???');
end