Detecting geographic clusters

Question

I have a R data.frame containing longitude, latitude which spans over the entire USA map. When X number of entries are all within a small geographic region of say a few degrees longitude & a few degrees latitude, I want to be able to detect this and then have my program then return the coordinates for the geographic bounding box. Is there a Python or R CRAN package that already does this? If not, how would I go about ascertaining this information?

Answer 1

I was able to combine Joran's answer along with Dan H's comment. This is an example ouput:

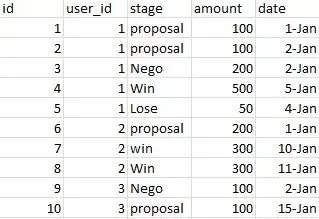
The python code emits functions for R: map() and rect(). This USA example map was created with:

map('state', plot = TRUE, fill = FALSE, col = palette())

and then you can apply the rect()'s accordingly from with in the R GUI interpreter (see below).

import math
from collections import defaultdict

to_rad = math.pi / 180.0   # convert lat or lng to radians
fname = "site.tsv"        # file format: LAT\tLONG
threshhold_dist=50         # adjust to your needs
threshhold_locations=15    # minimum # of locations needed in a cluster

def dist(lat1,lng1,lat2,lng2):
    global to_rad
    earth_radius_km = 6371

    dLat = (lat2-lat1) * to_rad
    dLon = (lng2-lng1) * to_rad
    lat1_rad = lat1 * to_rad
    lat2_rad = lat2 * to_rad

    a = math.sin(dLat/2) * math.sin(dLat/2) + math.sin(dLon/2) * math.sin(dLon/2) * math.cos(lat1_rad) * math.cos(lat2_rad)
    c = 2 * math.atan2(math.sqrt(a), math.sqrt(1-a)); 
    dist = earth_radius_km * c
    return dist

def bounding_box(src, neighbors):
    neighbors.append(src)
    # nw = NorthWest se=SouthEast
    nw_lat = -360
    nw_lng = 360
    se_lat = 360
    se_lng = -360

    for (y,x) in neighbors:
        if y > nw_lat: nw_lat = y
        if x > se_lng: se_lng = x

        if y < se_lat: se_lat = y
        if x < nw_lng: nw_lng = x

    # add some padding
    pad = 0.5
    nw_lat += pad
    nw_lng -= pad
    se_lat -= pad
    se_lng += pad

    # sutiable for r's map() function
    return (se_lat,nw_lat,nw_lng,se_lng)

def sitesDist(site1,site2): 
    #just a helper to shorted list comprehension below 
    return dist(site1[0],site1[1], site2[0], site2[1])

def load_site_data():
    global fname
    sites = defaultdict(tuple)

    data = open(fname,encoding="latin-1")
    data.readline() # skip header
    for line in data:
        line = line[:-1]
        slots = line.split("\t")
        lat = float(slots[0])
        lng = float(slots[1])
        lat_rad = lat * math.pi / 180.0
        lng_rad = lng * math.pi / 180.0
        sites[(lat,lng)] = (lat,lng) #(lat_rad,lng_rad)
    return sites

def main():
    sites_dict = {}
    sites = load_site_data()
    for site in sites: 
        #for each site put it in a dictionary with its value being an array of neighbors 
        sites_dict[site] = [x for x in sites if x != site and sitesDist(site,x) < threshhold_dist] 

    results = {}
    for site in sites: 
        j = len(sites_dict[site])
        if j >= threshhold_locations:
            coord = bounding_box( site, sites_dict[site] )
            results[coord] = coord

    for bbox in results:
        yx="ylim=c(%s,%s), xlim=c(%s,%s)" % (results[bbox]) #(se_lat,nw_lat,nw_lng,se_lng)
        print('map("county", plot=T, fill=T, col=palette(), %s)' % yx)
        rect='rect(%s,%s, %s,%s, col=c("red"))' % (results[bbox][2], results[bbox][0], results[bbox][3], results[bbox][2])
        print(rect)
        print("")

main()

Here is an example TSV file (site.tsv)

LAT     LONG
36.3312 -94.1334
36.6828 -121.791
37.2307 -121.96
37.3857 -122.026
37.3857 -122.026
37.3857 -122.026
37.3895 -97.644
37.3992 -122.139
37.3992 -122.139
37.402  -122.078
37.402  -122.078
37.402  -122.078
37.402  -122.078
37.402  -122.078
37.48   -122.144
37.48   -122.144
37.55   126.967

With my data set, the output of my python script, shown on the USA map. I changed the colors for clarity.

rect(-74.989,39.7667, -73.0419,41.5209, col=c("red"))
rect(-123.005,36.8144, -121.392,38.3672, col=c("green"))
rect(-78.2422,38.2474, -76.3,39.9282, col=c("blue"))

---

Addition on 2013-05-01 for Yacob

---

These 2 lines give you the over all goal...

map("county", plot=T )
rect(-122.644,36.7307, -121.46,37.98, col=c("red"))

If you want to narrow in on a portion of a map, you can use ylim and xlim

map("county", plot=T, ylim=c(36.7307,37.98), xlim=c(-122.644,-121.46))
# or for more coloring, but choose one or the other map("country") commands
map("county", plot=T, fill=T, col=palette(), ylim=c(36.7307,37.98), xlim=c(-122.644,-121.46))
rect(-122.644,36.7307, -121.46,37.98, col=c("red"))

You will want to use the 'world' map...

map("world", plot=T )

It has been a long time since I have used this python code I have posted below so I will try my best to help you.

threshhold_dist is the size of the bounding box, ie: the geographical area
theshhold_location is the number of lat/lng points needed with in
    the bounding box in order for it to be considered a cluster.

Here is a complete example. The TSV file is located on pastebin.com. I have also included an image generated from R that contains the output of all of the rect() commands.

# pyclusters.py
# May-02-2013
# -John Taylor

# latlng.tsv is located at http://pastebin.com/cyvEdx3V
# use the "RAW Paste Data" to preserve the tab characters

import math
from collections import defaultdict

# See also: http://www.geomidpoint.com/example.html
# See also: http://www.movable-type.co.uk/scripts/latlong.html

to_rad = math.pi / 180.0  # convert lat or lng to radians
fname = "latlng.tsv"      # file format: LAT\tLONG
threshhold_dist=20        # adjust to your needs
threshhold_locations=20   # minimum # of locations needed in a cluster
earth_radius_km = 6371

def coord2cart(lat,lng):
    x = math.cos(lat) * math.cos(lng)
    y = math.cos(lat) * math.sin(lng)
    z = math.sin(lat)
    return (x,y,z)

def cart2corrd(x,y,z):
    lon = math.atan2(y,x)
    hyp = math.sqrt(x*x + y*y)
    lat = math.atan2(z,hyp)
    return(lat,lng)

def dist(lat1,lng1,lat2,lng2):
    global to_rad, earth_radius_km

    dLat = (lat2-lat1) * to_rad
    dLon = (lng2-lng1) * to_rad
    lat1_rad = lat1 * to_rad
    lat2_rad = lat2 * to_rad

    a = math.sin(dLat/2) * math.sin(dLat/2) + math.sin(dLon/2) * math.sin(dLon/2) * math.cos(lat1_rad) * math.cos(lat2_rad)
    c = 2 * math.atan2(math.sqrt(a), math.sqrt(1-a)); 
    dist = earth_radius_km * c
    return dist

def bounding_box(src, neighbors):
    neighbors.append(src)
    # nw = NorthWest se=SouthEast
    nw_lat = -360
    nw_lng = 360
    se_lat = 360
    se_lng = -360

    for (y,x) in neighbors:
        if y > nw_lat: nw_lat = y
        if x > se_lng: se_lng = x

        if y < se_lat: se_lat = y
        if x < nw_lng: nw_lng = x

    # add some padding
    pad = 0.5
    nw_lat += pad
    nw_lng -= pad
    se_lat -= pad
    se_lng += pad

    #print("answer:")
    #print("nw lat,lng : %s %s" % (nw_lat,nw_lng))
    #print("se lat,lng : %s %s" % (se_lat,se_lng))

    # sutiable for r's map() function
    return (se_lat,nw_lat,nw_lng,se_lng)

def sitesDist(site1,site2): 
    # just a helper to shorted list comprehensioin below 
    return dist(site1[0],site1[1], site2[0], site2[1])

def load_site_data():
    global fname
    sites = defaultdict(tuple)

    data = open(fname,encoding="latin-1")
    data.readline() # skip header
    for line in data:
        line = line[:-1]
        slots = line.split("\t")
        lat = float(slots[0])
        lng = float(slots[1])
        lat_rad = lat * math.pi / 180.0
        lng_rad = lng * math.pi / 180.0
        sites[(lat,lng)] = (lat,lng) #(lat_rad,lng_rad)
    return sites

def main():
    color_list = ( "red", "blue", "green", "yellow", "orange", "brown", "pink", "purple" )
    color_idx = 0
    sites_dict = {}
    sites = load_site_data()
    for site in sites: 
        #for each site put it in a dictionarry with its value being an array of neighbors 
        sites_dict[site] = [x for x in sites if x != site and sitesDist(site,x) < threshhold_dist] 

    print("")
    print('map("state", plot=T)') # or use: county instead of state
    print("")


    results = {}
    for site in sites: 
        j = len(sites_dict[site])
        if j >= threshhold_locations:
            coord = bounding_box( site, sites_dict[site] )
            results[coord] = coord

    for bbox in results:
        yx="ylim=c(%s,%s), xlim=c(%s,%s)" % (results[bbox]) #(se_lat,nw_lat,nw_lng,se_lng)

        # important!
        # if you want an individual map for each cluster, uncomment this line
        #print('map("county", plot=T, fill=T, col=palette(), %s)' % yx)
        if len(color_list) == color_idx:
            color_idx = 0
        rect='rect(%s,%s, %s,%s, col=c("%s"))' % (results[bbox][2], results[bbox][0], results[bbox][3], results[bbox][1], color_list[color_idx])
        color_idx += 1
        print(rect)
    print("")


main()

Answer 2

I'm doing this on a regular basis by first creating a distance matrix and then running clustering on it. Here is my code.

library(geosphere)
library(cluster)
clusteramounts <- 10
distance.matrix <- (distm(points.to.group[,c("lon","lat")]))
clustersx <- as.hclust(agnes(distance.matrix, diss = T))
points.to.group$group <- cutree(clustersx, k=clusteramounts)

I'm not sure if it completely solves your problem. You might want to test with different k, and also perhaps do a second run of clustering of some of the first clusters in case they are too big, like if you have one point in Minnesota and a thousand in California. When you have the points.to.group$group, you can get the bounding boxes by finding max and min lat lon per group.

If you want X to be 20, and you have 18 points in New York and 22 in Dallas, you must decide if you want one small and one really big box (20 points each), if it is better to have have the Dallas box include 22 points, or if you want to split the 22 points in Dallas to two groups. Clustering based on distance can be good in some of these cases. But it of course depend on why you want to group the points.

/Chris

Answer 3

A few ideas:

• Ad-hoc & approximate: The "2-D histogram". Create arbitrary "rectangular" bins, of the degree width of your choice, assign each bin an ID. Placing a point in a bin means "associate the point with the ID of the bin". Upon each add to a bin, ask the bin how many points it has. Downside: doesn't correctly "see" a cluster of points that stradle a bin boundary; and: bins of "constant longitudinal width" actually are (spatially) smaller as you move north.
• Use the "Shapely" library for Python. Follow it's stock example for "buffering points", and do a cascaded union of the buffers. Look for globs over a certain area, or that "contain" a certain number of original points. Note that Shapely is not intrinsically "geo-savy", so you'll have to add corrections if you need them.
• Use a true DB with spatial processing. MySQL, Oracle, Postgres (with PostGIS), MSSQL all (I think) have "Geometry" and "Geography" datatypes, and you can do spatial queries on them (from your Python scripts).

Each of these has different costs in dollars and time (in the learning curve)... and different degrees of geospatial accuracy. You have to pick what suits your budget and/or requirements.

Answer 4

if you use shapely, you could extend my cluster_points function to return the bounding box of the cluster via the .bounds property of the shapely geometry , for example like this:

clusterlist.append(cluster, (poly.buffer(-b)).bounds)

Answer 5

maybe something like

def dist(lat1,lon1,lat2,lon2):
    #just return normal x,y dist
    return sqrt((lat1-lat2)**2+(lon1-lon2)**2)

def sitesDist(site1,site2):
    #just a helper to shorted list comprehensioin below
    return dist(site1.lat,site1.lon,site2.lat,site2.lon)
sites_dict = {}
threshhold_dist=5 #example dist
for site in sites:
    #for each site put it in a dictionarry with its value being an array of neighbors
    sites_dict[site] = [x for x in sites if x != site and sitesDist(site,x) < threshhold_dist]
print "\n".join(sites_dict)