Does every species get around a billion heartbeats on average?

Question

I read this webcomic today:

I have no idea where the author got his factoid about the billion heartbeats. But it sounds interesting. The examples I can think of (rabbits, humans, elephants, said hummingbird) seem to support the theory that bigger creatures both have a slower heartbeat and live longer. Is there really such a trend, or am I missing the counterexamples? And if yes, how close does it come to the "one billion" number?

Actually some parrots can live for 50+ years. And chickens are lucky to survive to maturity... — Chad, Aug 11 '11 at 15:32
I think the obvious answer is "No", since many species don't have hearts. — fred, Aug 18 '11 at 19:18
A long time ago, Isaac Asimov wrote a regular article for Fantasy & Science Fiction magazine, and most were collected into books. In one of those, he calculated lifetime in heartbeats for a lot of animals, and concluded that everybody except humans had about a billion-heartbeat maximum lifetime, but humans hit four billion. (The methodology was flawed; he calculated max human lifetime as 114 years, and all other species got less atypical maxima.) — David Thornley, Aug 19 '11 at 03:07
What about molluscs? The octopus has three hearts! So we should count all the heart beats, no? — Nicolas Barbulesco, Aug 25 '15 at 11:04
All mammals do live for about a billion heartbeats (rate mostly determined by size). Asimov calculation is reproduced at the end of his book "A Choice of Catastrophes". (The human AVERAGE one or two hundred years ago was probably also close to a billion, considering overall lower mortality from accidents and infant causes.) Average industrial human lifespan today would work to about 3 billion, with some exceptional humans getting to 4 billion heartbeats. (According to Asimov calculations, I don't know if they are original.) — fred, Jun 04 '22 at 20:32
Athletes have lower resting heartrates. The correlates with the finding that regular exercise may increase lifespan by around ten percent. (However other conflicting habits *may* show greater increases.) — fred, Jun 04 '22 at 20:38

score 148 · Answer 1 · edited Jun 17 '20 at 09:41

148

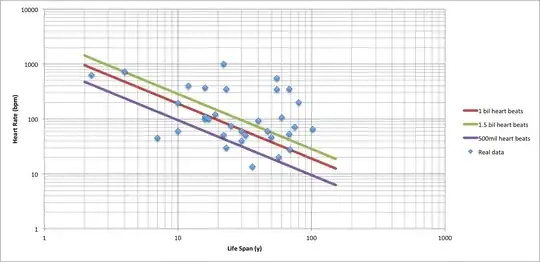
YES, there is some truth behind the "1 billion heartbeats " claim.
And when I say "some" I mean the creator of the comic didn't just make it up out of thin air.

While it's not literally true that all animals get 1 billion heartbeats before they die, a relation between metabolic rate (which is related to heart rate) and life span has been observed.

San José State University - Animal Longevity and Scale:

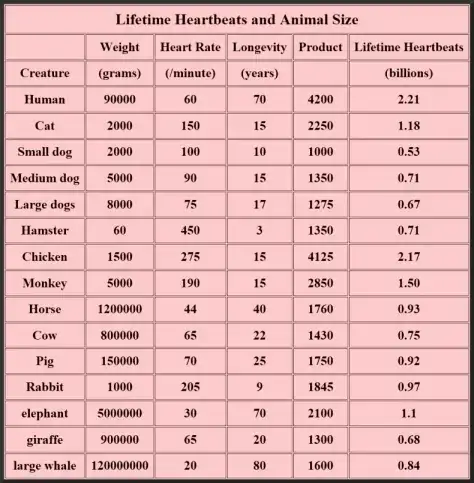
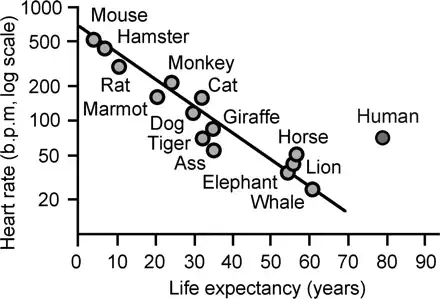
Heart rate and life expectancy in mammals and humans:

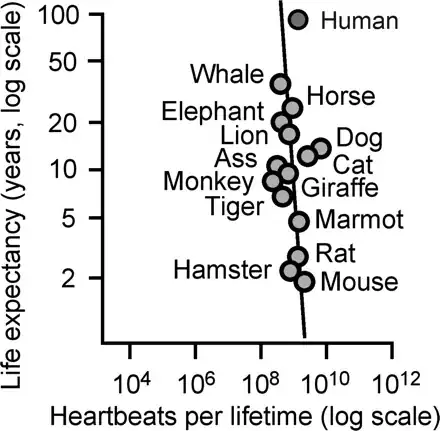
Life expectancy and total heart beats per lifetime in mammals and humans:

As a corollary, the basal energy consumption per heart beat and heart mass may be the same for all animals.

This suggests that the life span is predetermined by the basic energetics of the living cells, and that the apparent inverse relation between life span and heart rate reveals the heart rate to serve as a marker of the metabolic rate.

This may be exemplified by considering the vast range of physiological cardiac parameters between one of the smallest, the shrew weighing 2 g, and the largest extant mammalian, the blue whale of 100 000 kg.

Despite a difference of many millions in body weight, heart weight, stroke volume, and total blood pumped per lifetime, the total oxygen consumption and ATP usage per unit mass and lifetime are almost identical together with the total number of the heart beats per lifetime.

[Source]

Mice and Elephants: A Matter of Scale

As animals get bigger, from tiny shrew to huge blue whale, pulse rates slow down and life spans stretch out longer, conspiring so that the number of heartbeats during an average stay on Earth tends to be roughly the same, around a billion.

Mysteriously, these and a large variety of other phenomena change with body size according to a precise mathematical principle called "quarter-power scaling".

[...]

It might seem that because a cat is a hundred times more massive than a mouse, its metabolic rate, the intensity with which it burns energy, would be a hundred times greater. After all, the cat has a hundred times more cells to feed.

But if this were so, the animal would quickly be consumed by a fit of spontaneous feline combustion, or at least a very bad fever. The reason: the surface area a creature uses to dissipate the heat of the metabolic fires does not grow as fast as its body mass.

To see this, consider a mouse as an approximation of a small sphere. As the sphere grows larger, to cat size, the surface area increases along two dimensions but the volume increases along three dimensions. The size of the biological radiator cannot possibly keep up with the size of the metabolic engine.

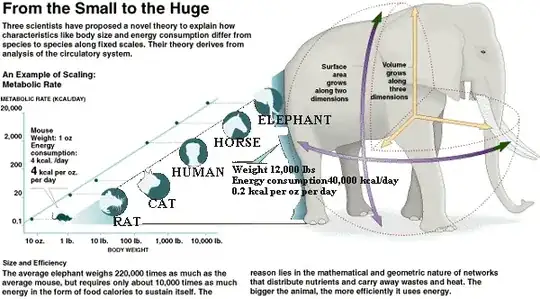
Things behave differently at different scales, but there are orderly ways -- scaling laws -- that connect one realm to another.

Metabolic Rate and Kleiber's Law:

The first accurate measurements of body mass versus metabolic rate in 1932 shows that the metabolic rate R for all organisms follows the 3/4 power-law of the body mass,

R ~ M^3/4

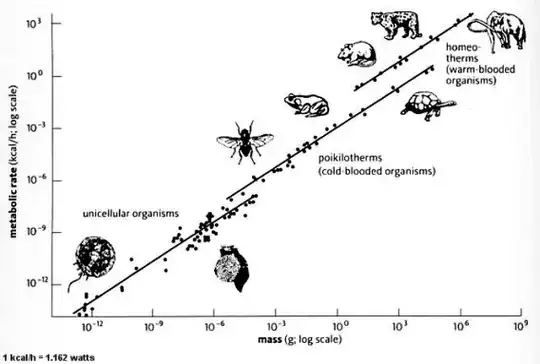
This is known as the Kleiber's Law.

The reasons behind the power law are not yet fully understood, although there are of course theories. But since the OP's question doesn't actually ask for an explanation I feel it's okay to leave it to the interested reader to click through the links above and below to learn more about the proposed theories (plus, I believe it would make my answer just unbearably long if I include them in my post).

More:

Biophysics - New Clues to Why Size Equals Destiny
Life's Universal Scaling Laws [PDF ]
Phylogeny and metabolic scaling in mammals [PDF ]
Rest heart rate and life expectancy [Abstract ]
Similarity in the number of lifespan heartbeats among non-hibernating homeothermic animals [Abstract ]
Animal Life Spans

edited Jun 17 '20 at 09:41

Community

1

answered Aug 11 '11 at 09:29

Oliver_C

47,851
18
213
208

5

I am already impressed with the nonimproved version, but being an informavore, I'd be happy to see the improved version too. – rumtscho Aug 11 '11 at 09:38
2

@Oliver_C: Is the life expectancy of the dog/cat for one in captivity, or the wild? I seem to recall domesticated animals living quite a bit longer in captivity. – Brian M. Hunt Aug 11 '11 at 12:44
12

I immediately notice that the first graph suggests that dogs and cats live 30 years. Definitely not true. Pet dogs live around 10-14, cats a few years more. The second graph seems to correct this, although they're reversed in this case (cats live longer). – Tesserex Aug 11 '11 at 13:30
The second graph verifies that the statement in the OP is true. However, the speculation about the interpretation seems ill-founded to me. – Aug 11 '11 at 15:02
1

Interestingly its only been in the last few hundred years that human life expectancy has increased to this point. Move back to before we learned medicine especially antibiotics and we are back inline. The other 2 near outliers are dogs and cats animals whom we tend to provide some medical care. – Chad Aug 11 '11 at 15:30
7

Please note that the second graph uses log scales which are probably making something appear out of nothing... – Sklivvz Aug 11 '11 at 16:10
@Brian - I assume it's "captivity", but wether it's 15 or 30 years (for a cat), the numbers for "hearbeats in a lifetime" will be pretty much in the same order of magnitude. – Oliver_C Aug 11 '11 at 20:18
1

@Tesserex - Cats lving 30 years are certainly not the norm, but possible. ["Creme Puff" was 38 when she died](http://en.wikipedia.org/wiki/Creme_Puff_(cat)) – Oliver_C Aug 11 '11 at 20:20
10

Wow, talk about creating a signal out of noise. Your table shows that it's 1 billion +/- 1/2 a billion or more. 1 billion +/- 50+% isn't very precise. Not only that it shows a ridiculously small number of animals. The last chart is completely different, having nothing at all to do with number of heartbeats (though interesting). The defense of being right to "an order of magnitude" is also very weak. "Within an order of magnitude" is pretty sloppy from a scientific standpoint. – Russell Steen Aug 11 '11 at 22:58
@Russell - The problem with "number of heartbeats" is that the lifespan depends on so many factors. So it's no surprise that you don't get exactly 1 billion for everyone. Therefore looking at "metabolic rate" (which is related to heart rate) makes more sense. And there seems to indeed be an observable phenomenon (power law) that shows that there is a (evolutionary) connection between the small and the large. – Oliver_C Aug 12 '11 at 06:54
2

@Oliver_C I understood the concern to be not about in which order of magnitude the cat data point belongs, but rather whether the graph is to be trusted at all. Thirty years is nowhere near the *average* lifespan of a cat, and with an error so glaring as to distract us from the graph's intent, you have to wonder what else is wrong about it. As your answer stands now, you've presented a table with data that flagrantly contradicts the graph it immediately precedes. – Corey Aug 12 '11 at 12:43
1

@Oliver_C -- Yes, looking at metabolic rate makes a lot more sense. I agree entirely on that point. But that's not the question posed. Asserting that the myth is true and then using metabolic rate as supporting evidence is rather misleading. – Russell Steen Aug 12 '11 at 13:29
@Corey - The numbers for lifespan can vary quite a lot. So, if one uses different sources one can end up getting different numbers. – Oliver_C Aug 12 '11 at 13:36
@Russell - I don't say the myth is true, I say there is some truth to it, meaning it's not made up out of the blue, but there is a science behind it. The metabolic rate is part of the explanation. Why do large animals, in general, live longer and have a lower heart rate? - Yes, +/-50% sounds like a lot, but look at it from this point: the lifespans in the table above vary between "3 and 80 years", that's a difference factor of __26.7__. The heartbeat numbers vary between "0.53 and 2.21", a difference factor of __4.2__. – Oliver_C Aug 12 '11 at 13:50
15

We are talking about physiology here, not particle physics. Individual differences of 50% are not so uncommon. Just to take a random example, normal plasma glucose levels range between 3 and 8 mmol/l. So that's an average of 5.5 +/- 2.5...And for many hormones the range is way larger. – nico Aug 12 '11 at 15:16
If Kleiber's law is true and the heartrate/lifespan correlation is also true than there has to be a size lifespan correlation as well. There are small tortoises with pretty long lifespans. – Christian Aug 12 '11 at 15:33
2

@Oliver_C And I'm saying that a source that claims an *average lifespan* of more than thirty years for cats should be approached with a great deal of skepticism. You want us to just accept that graph as truth? How many cats do you know that are over thirty years old? – Corey Aug 12 '11 at 17:13
@Corey - I don't expect you to accept anything. You are free to question any data/source I or anyone else posts here. I would say this site actually encourages people to do so. – Oliver_C Aug 12 '11 at 18:19
1

@Christian - Would you say small animals with a long lifespan are the rule or the exception? – Oliver_C Aug 12 '11 at 18:23
1

Many [crows](http://en.wikipedia.org/wiki/Corvus_(genus)) are quite small and their lifetime is about the same as the human have. – Suma Aug 12 '11 at 19:35
1

Crow heart rate is 345 bpm - see [A Bird's Heart and Blood](http://www.earthlife.net/birds/blood.html) or [RESPIRATORY AND HEART RATES OF BIRDS AT REST](http://elibrary.unm.edu/sora/Condor/files/issues/v070n04/p0358-p0365.pdf) when resting. With 70 years of life this gives 1.2e10 heartbeats. – Suma Aug 12 '11 at 19:50
The study [you have referenced for mammals](http://www.ncbi.nlm.nih.gov/pubmed/9316546) says in the abstract " remarkably constant and average 7.3 +/- 5.6 x 10(8) heart beats/lifetime" - which translates to 0.17 - 1.29 x 1e9. I would not call that "constant", but if true, I admit it is much less varied the e.g. body mass, or the life expectancy measured as a time. – Suma Aug 12 '11 at 20:06
@Oliver_C I am merely asking if you believe your own evidence, which I think is a fair question. Or, how absurd would a data set have to be before you consider it to be detrimental to those seeking an answer? Presenting data that suggests a cat's life expectancy to be more than twice that of an *actual* cat's is only blemishing your answer. – Corey Aug 12 '11 at 20:33
@Corey - I have read a lot of papers and flubs happen. Wether or not a flub bothers me depends on it's relevance. In this case, changing the cat's 30 to 15 wouldn't change the graph in such a profound way that it leads to a different conclusion. It's not like everything hinges on it being 30 instead of 15. – Oliver_C Aug 12 '11 at 22:38
@Suma - Ageing is a complex matter that is influenced by many factors. That larger animals tend to live longer than smaller animals is therefore not an absolute rule. Why it doesn't apply to certain animals is indeed a matter of debate and research. Which is why I pointed out that this phenomenon is not yet fully understood. – Oliver_C Aug 12 '11 at 22:46
1

@Oliver_C Sorry if I was unclear. It is fair to say that the conclusions drawn from the graph would not change if you move the cat data point from 30 years to 15. What I mean is that someone looking for an answer and seeing such a flub might wonder what else in the graph is off by a factor of more than two and give it (and possibly your answer) less credibility. That's all. – Corey Aug 12 '11 at 23:03
1

@oli Imo your answer needs better numbers and a better statistical analysis. All that we can derive from the data currently is that animals live 10y and have a heartbeat of 100bpm, within +/- an order of magnitude... :) – Sklivvz Aug 13 '11 at 07:25
@Cory - I absolutely agree that a flub should raise flags and make one suspicious. But I think one should also evaluate the severity of the flub before condemning the whole paper. Some flubs do have a significant consequences, others not so much. – Oliver_C Aug 13 '11 at 11:23
3

@Sklivvz - Maybe I should add the [immortal jellyfish](http://en.wikipedia.org/wiki/Turritopsis_nutricula) ;) - I don't think there is much of a disbute about larger animals tending to live longer and that there is a connection with the metabolism. What __is__ debated is how much does metabolism influence lifespan (it is for sure not the sole factor) and how exactly does it work? – Oliver_C Aug 13 '11 at 11:45
I always thought small dogs lived longer than large dogs?? – Nikko Jan 15 '15 at 18:36
1

Animals used in table are all mammals what about other classes or this rule to be around 10^9 is only for mammals? – Matas Vaitkevicius Jan 13 '16 at 16:16
I think using a logarithmic scale on a line chart makes the relation ship look much more direct and straightforward than it actually is. It seems a bit dishonest. – PoloHoleSet Apr 24 '23 at 17:11

Russell Steen · Answer 2 · 2011-08-15T19:46:16.260

No, this is not true. The Daphniidae only live for about 18.2 million heartbeats, which isn't even close to the (very loose) criteria of "within an order of magnitude". There are other species as well. All animals just do not have "around a billion" heartbeats.

A good mammalian counter example is the North American black bear. Even when not hibernating they only have about 55 beats per minute and only live around 25 years. Even if it never hibernated, that's only 700 million beats per lifetime. When they hibernate their heartrate slows to 14 beats per minute for up to seven months. Even on a short hibernation season of only 5 months (every year for their entire lifespan) they'd get only 500 million beats.

The rumor you found hit the "main stream" with an USA today story and is just one of those trendy things to say at a cocktail party to sound smart.

It doesn't help that this whole thing gets mixed up with metabolic rate, which is not the same thing as heart rate. Most of the actual research is about things like metabolic rate, production of free radicals, etc. If you read this abstract used by that story you'll see that it's talking about metabolic rate (usually lumped together as 'rate of living') and even that is strongly challenged because actual observations tend to conflict with the conclusions of the theory. The abstract also makes it very clear that this isn't a matter where there is yet a clear answer.

A more accurate statement may be "All the animals a news reporter could think to look up were somewhere in the same vague vicinity of a billion heartbeats". Or for a better explanation of how this became news...

You are of course right that not all animals die after "1 billion heartbeats". That's why I said "_some truth_ " in my answer. The "1 billion heartbeats" is basically the flashy and simplified main stream version of the underlying "metabolic rate is not independent of body mass" phenomenon. — Oliver_C, Aug 12 '11 at 07:14
Well, there's "some truth" in almost anything by that criteria. You can find a handful of data points that will support *any* theory and say there's "some truth" to it... but that's not science. — Russell Steen, Aug 12 '11 at 13:30
To be clear, I do think your answer has some interesting and worthwhile information in it, but that the op's question is more directly and easily disproven as clearly not every species has around a billion beats, and there's not even enough convergence IMO to justify an "almost every" assertion. — Russell Steen, Aug 12 '11 at 13:40
Okay, I see now that we look at the OP's question differently. I don't take it as literally as you. You are correct that the "1 billion" is not striclty true. I will change my answer to make it more clear what I mean. — Oliver_C, Aug 12 '11 at 14:00
For the north american black bear, 700 M heart beats are roughly 1 G. Even 500 M are half, this is "quite" near. — Nicolas Barbulesco, Aug 25 '15 at 08:33

score 30 · Answer 3 · edited Jun 17 '20 at 09:41

30

It's true within 50% error for mammals and the study that started this idea is the following:

Rest heart rate and life expectancy

Among mammals, there is an inverse semilogarithmic relation between heart rate and life expectancy. The product of these variables, namely, the number of heart beats/lifetime, should provide a mathematical expression that defines for each species a predetermined number of heart beats in a lifetime. Plots of the calculated number of heart beats/lifetime among mammals against life expectancy and body weight (allometric scale of 0.5 x 10(6)) are, within an order of magnitude, remarkably constant and average 7.3 +/- 5.6 x 10(8) heart beats/lifetime.

However, I did not find this article straight away, so I've created my own plot and data set. Guess what? I've found that the conclusions of the above article are actually quite wrong when extended to non-mammalian species. I got most of my data from peer-reviewed literature.

The results can be read on the following diagram:

lifespan vs heartbeat
^{Full size}

How to read the chart

The red line marks where the all the data points should be if this hypothesis were true
The green and violet lines mark the ±50% lines. According to the study above all mammals fall within those two lines.
Anything outside the lines pretty much disproves the hypothesis

Discussion

Clearly reptilians, birds, insect and mammals do not share the same heart physiology. So expecting the same kind of mileage is unjustified.

Compare for example the canary and the elk: both have the same life-expectancy of 22 years, but the former has a heartbeat of ~1000bpm, whereas the latter ~50bpm. Therefore it follows that a canary's heart will beat 20 times more than the heart of an elk. There are many examples like this in the data set.

Dataset

The dataset is available here (along with 32 references).

There was no way of making it fit in here.

edited Jun 17 '20 at 09:41

Community

1

answered Aug 13 '11 at 20:35

Sklivvz

78,578
29
321
428

5

+1 for doing extensive research to create your own graph. - There is such large variety in the animal kingdom, e.g. from the small to the big, body mass encompasses at least 6 orders of magnitude. A canary and a whale differ in mass by factor of ~1 million. But their number of total heartbeats differs only by a factor of ~10. I find it intriguing that despite all their differences most animals fall in between the 10e8 - 10e10 range. – Oliver_C Aug 14 '11 at 01:25
@oli if you pick a number at random between 1 and 100 for life span and another between 10 and 100 for heart rate, 90% of the results will be within 2 orders of magnitude (unless I'm mistaken). This means that the available possible ranges for the parameters are the real concerns here. – Sklivvz Aug 14 '11 at 16:29
3

Yes. This begs the question why are those numbers as they are? - And when you multiply two variables that each vary by 2 orders of magnitude, the product should vary by 4 orders of magnitude. Unless the variables are not independant of each other and there is some sort of inverse relationship. – Oliver_C Aug 15 '11 at 12:33
3

@oli The product of two uniform random variables is not a uniform random variable. The *range of possible products* will span 4 orders of magnitude, but the distribution of probabilities will be lumped up in the middle, thus reducing the effective range of orders of magnitude. Add to that that the initial variables will not be really uniform, but likely normal and thus the lumping effect will be even greater. I am looking for some links to explain this further. – Sklivvz Aug 15 '11 at 15:34
1

No need for the extra work, I understand what you mean: the extremes are less likely (but that should also be valid for the other side of the equation). - The smaller "lumps" might encompass only 1 order of magnitude, but their product will encompass 2. To avoid a spread you'll need some kind of inverse relationship between the variables. – Oliver_C Aug 15 '11 at 16:33
"It's true within 50% error" -- err ... wow, just ... wow. I understand so much about things now that I understand that a 50% error rate is considered valid from which to draw conclusions. – Russell Steen Aug 15 '11 at 19:44
Indeed @rus, indeed... That's exactly how the article puts it (and I've also found other peer-reviewed articles with the same sort of claims..) – Sklivvz Aug 15 '11 at 21:46
1

Says a lot about the state of "peer-review" in science and what that's worth. – Russell Steen Aug 15 '11 at 22:40
"The product of these variables, namely, the number of heart beats/lifetime" This is not the product, this is the division! – Nicolas Barbulesco Aug 25 '15 at 10:28
"within 50% error" - so.... good enough for newspaper "science" articles or political discourse. Got it. – PoloHoleSet Sep 27 '16 at 15:04
@NicolasBarbulesco: Employ some dimensional analysis and you will see that the statement quoted is quite correct, and you are wrong. – Ben Voigt Oct 03 '16 at 22:50

rumtscho · Answer 4 · 2023-04-21T12:33:36.320

By now, I have read multiple books in which the authors take for granted that a simple mathematical relationship exists between size and metabolism (sometimes measured in heartbeats) except for humans, who are surprisingly long-lived for their size. The modern research on that topic has been spearheaded by Geoffrey West, whose book "Scale" I have put on my reading list. I don't have the exact formula at hand. But I would count the claim as "true" even if the number "a billion heartbeats" might be a wrong-but-placative retelling.

Curiously, today I was reading an older popular science book and it contained a chapter dedicated to that relationship.

This states that the ratio of breath time to heartbeat time is 4.0 in mammals of any body size. In other words, all mammals, whatever their size, breathe once for each four heartbeats. Small mammals breathe and beat their hearts faster than large mammals, but both breath and heart slow up at the same relative rate as mammals get larger.

Lifetime also scales at the same rate as body weight (.28 times as fast as we move from small to large mammals). This means that the ratio of both breath time and heartbeat time to lifetime is also constant over the entire range of mammalian size. When we perform a calculation similar to the one above, we find that all mammals, regardless of their size, tend to breathe about 200 million times during their lives (their hearts, therefore, beat about 800 million times). Small mammals breathe fast, but live for a short time. Measured by the internal clocks of their own hearts or the rhythm of their own breathing, all mammals live the same time.

It states that one of the first people to note the existence of such relationships was Galileo, but that the methods for empirical calculation were developed by "W. R. Stahl, B. Günther, and E. Guerra in the late 1950s and early 1960s".

The numbers the chapter discusses are about mammals, but it also makes a qualitative claim that the relationship holds for many other animals (except humans, which is explained by our evolutionary strategy of neoteny).

The source I am citing is Stephen Jay Gould's book "The panda's thumb", chapter 29, "Our allotted lifetimes".

Asimov remarks that it may be said that mouse packs as much living into his two years as the elephant does in his 70. — fred, Jun 04 '22 at 20:43

Does every species get around a billion heartbeats on average?

4 Answers4

Linked