17

I found this map from this substack, World in motion:

Rohan Chabukswar and Kushal Mukherjee, a pair of researchers at the United Technologies Research Center in Cork, plotted the route in 2018 in response to a question posed by Live Science. They worked out that, if you set off from the coast of Pakistan, it would be possible to sail for nearly 20,000 miles – between Africa and Madagascar, narrowly missing the coast of South America – before hitting land again in the far north east of Russia.

And although it looks like a curve on a two-dimensional map, your theoretical boat would actually be sailing in a completely straight line.

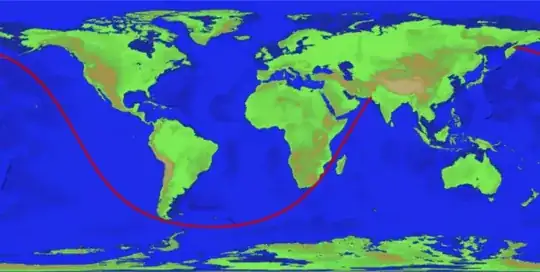
sine-like wave headed from Pakistan, between Madagascar and Africa, below South America, to east Russia

It claims you can sail from north east Russia to Pakistan in a straight line. How is this true?

Oddthinking
  • 140,378
  • 46
  • 548
  • 638
Gandalf
  • 1,763
  • 3
  • 12
  • 14
  • 80
    How is this a question that requires skeptical inquiry? A simple physical or virtual globe will tell that the claim is plausible to the extent of being obvious. Anyway, I think earthscience.SE may be more suitable for this question as it is basically concerned with the interpretation of map projections. – Schmuddi Apr 25 '22 at 09:56
  • Cross-site near-duplicates on aviation.SE: [Why don't most planes fly in a straight path?](https://aviation.stackexchange.com/q/90717) / [Explaining a "Great Circle Route" to young Civil Air Patrol cadets](https://aviation.stackexchange.com/q/90567) – Peter Cordes Apr 27 '22 at 22:52

3 Answers3

96

An issue of Projection of a 3D globe on a 2D surface. It becomes immediately obvious once you look at an actual 3D globe that the line is, indeed, straight.

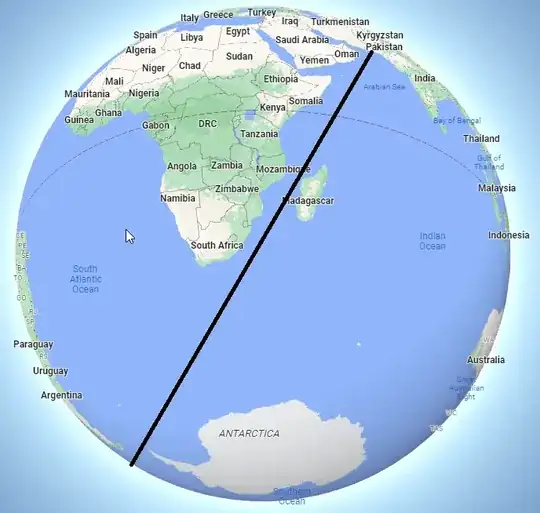
enter image description here

The other side is just lots of Pacific Ocean.

If you want the 3D view animated, this YT video shows that.

DevSolar
  • 19,034
  • 8
  • 77
  • 74
  • 16
    If this surprises you, check out "non-Euclidian geometry". Where a triangle does **not** have an angle sum of 180 degrees.;-) – DevSolar Apr 25 '22 at 14:08
  • 4
    I'm sure the answerer is already aware of this but the readers should note that even the above "proper 3D model" is still a projection and distorts countries: it's not a magic way of escaping the problems of map projections. The reason the straight line does actually appear straight in the above picture is that it goes through the centre. A great-circle (ie straight) path from, say, India to Paraguay on the above image would appear curved. – Dannie Apr 26 '22 at 14:20
  • 6
    @Dannie: And I took some time to rotate the virtual globe so that the line from Pakistan to between the Cape and Antarktika *would* go (more or less) through the center. A picture of a globe would have been easier, but I didn't feel like setting up for a cringey selfie in front of the mirror. Or defacing my globe with a sharpie. (Why is it so difficult to leave "good enough" alone? Once demonstrated in this way, it should be *obvious* that the claim is true, with the minor errors in the approximation of a "real" globe done by Google Maps being insignificant.) – DevSolar Apr 26 '22 at 14:24
  • Is this [Google Maps](https://www.google.com/maps/) or did you mean [Google Earth](https://earth.google.com/web/)? I can only get a sphere by zooming out in Earth, but not Maps. Can you actually get one on Maps? – terdon Apr 26 '22 at 16:23
  • @terdon [Not that it matters, in any way or form...](https://www.google.de/maps/@36.9231686,29.4062994,3.78z) – DevSolar Apr 26 '22 at 16:34
  • Oh, it doesn't matter at all! Sorry, I didn't mean to imply there was anything wrong with your answer or anything. I have already upvoted your answer which has all of the information needed to answer the question. I was just asking out of curiosity since I cannot get GMaps to show me a sphere. I guess it must be OS and/or browser-dependent since I tried brave, Chromium, Firefox and Chrome on Arch Linux and none of them supported it. Nor did my Android. So it must be a Windows/macOS/iOS thing instead. Thanks! – terdon Apr 26 '22 at 16:38
  • 5
    @terdon The sphere doesn't appear automatically when you zoom out (I'm sure it used to) but is available as an option at any zoom level - click "Layers", then "More", then "Globe View". – IMSoP Apr 26 '22 at 19:32
  • @Dannie And I believe the general solution to describe "straight line" in 3D involves the word "geodesics" a lot and would require a differential geometer to be present at the scene. – Silvio Mayolo Apr 26 '22 at 20:30
  • This answer is very vulnerable to link rot. Without clicking on any of them, I have no idea if the answer is yes or no. – Mindwin Remember Monica Apr 26 '22 at 20:33
55

What they are saying is that, if you leave Kamchatka in the correct direction, you can sail to Pakistan without changing the rudder setting. It does not mean you will always follow the same compass heading, you emphatically will not.

The reason is that a "straight" line on a sphere is what's called a "great circle". If you cut a sphere with a plane that goes through the centre of the sphere, the line it traces on the surface is a great circle.

A great circle is considered a straight line, because it is the shortest distance between 2 points, as long as you can't leave the surface of the sphere. All great circles on a sphere are the same size. Meridians are great circles, but lines of latitude (except the equator) are not.

Airplanes flying long distance follow great circles, to minimise fuel use. A flight from Seattle to London will pass over Greenland; planes going to Sydney from Santiago sometimes (depending on winds) fly far enough south to make Antarctica visible. They fly a "straight" line around the earth. For more details, see Flight Paths and Great Circles – Why Are Great Circles the Shortest Flight Path?.

You may have noticed that the path of satellites, projected on the surface, follows a similar curve. See, for example, the path of the International Space Station. While the path of the ISS is not circular, compared to the radius of the earth, the difference is minimal. The ISS obviously does not ever deviate from a straight line around the earth, yet, around it goes. With the ISS, the curve shifts from one orbit to the next, because the earth rotates underneath. If you extend the curve on your map, you'll notice it gets you back to Kamchatka.

The real problem is that a sphere cannot be accurately mapped on a flat map. There are always distortions. It's those distortions that convert a straight line into what looks like a curve. Wikipedia has a good article on the various types of map projections and their pros and cons.

Laurel
  • 30,040
  • 9
  • 132
  • 118
hdhondt
  • 5,856
  • 1
  • 35
  • 26
  • 3
    +1 "great circle". The OP should look that up. – GEdgar Apr 25 '22 at 15:24
  • 1
    The *shortest* path between any two points on the surface of a sphere runs along a great circle. If you want to take that as a definition of "straight line" in that context then that's fine, but there are other kinds of paths that could also be considered straight. For example, any path that runs along the intersection of the sphere and an arbitrary plane (which includes, but is not limited to great circles). It's not clear to me whether the path in question does run along a great circle, though it looks like it might do. – John Bollinger Apr 25 '22 at 19:27
  • 14
    "you can sail to Pakistan without changing the rudder setting" -- that's not quite right in real world conditions due to currents, wind, etc. The "taut string on a globe" visualization is probably a better simplification of great circle arcs. – GrandOpener Apr 25 '22 at 20:15
  • 2
    @JohnBollinger: In order to drive along any of those other paths, you'd need to be turning the wheel. Assuming a perfect sphere, any time your car is driving straight, you're driving along a great circle. Mathematically we say that [all geodesics on a sphere are great circles](https://mathworld.wolfram.com/Geodesic.html). – BlueRaja - Danny Pflughoeft Apr 26 '22 at 01:10
  • 8
    "you can sail to Pakistan without changing the rudder setting" Great circle means not changing the rudder setting, but not changing the rudder setting doesn't mean great circle; it can mean any circle. "A great circle is considered a straight line, because it is the shortest distance between 2 points" Well, part of it is. – Acccumulation Apr 26 '22 at 02:02
  • 1
    @"If you want to take that as a definition of "straight line" in that context then that's fine" That's what the mathematical definition is. "but there are other kinds of paths that could also be considered straight." Not really. Any other path would lack properties that we think of as being "straight", such as being locally minimal (that is, there are paths that are shorter). "For example, any path that runs along the intersection of the sphere and an arbitrary plane (which includes, but is not limited to great circles)." So every circle is a straight line? – Acccumulation Apr 26 '22 at 02:06
  • 1
    *A great circle is considered a straight line, because it is the shortest distance between 2 points, as long as you can't leave the surface of the sphere*, that's slightly confusing/misleading in the context of the mapped route. The indicated route is quite a detour, because it follows the great circle for more than halfway around the Earth. A flight from northeastern Russia to Pakistan would not at all take the mapped route. In fact, it would depart in exactly the opposite direction. A ship would not take this route either; going through the Strait of Malacca is shorter. – gerrit Apr 26 '22 at 08:46
  • 1
    In fact the rudder setting would be **straight** the whole way (ignoring wind and water currents trying to blow you off course) – user253751 Apr 26 '22 at 08:47
  • @Acccumulation a great circle is the unique path where the rudder setting is constant and _straight_ the entire time though (although admittedly that is currently missing from the answer) – Tristan Apr 26 '22 at 09:32
  • 7
    @JohnBollinger there is no good reason to consider those lines straight. Great circles (and geodesics more generally), are the only way of generalising straight lines to curved surfaces – Tristan Apr 26 '22 at 09:32
  • 1
    it might also be worth noting that a line of constant compass heading is a rhumb-line, for OP to read more – Tristan Apr 26 '22 at 09:33
  • 3
    @JohnBollinger If you want to define "straight" to include "doing doughnuts", I suppose you *can*, but you're using it wildly different to how everybody else in the world uses the word, and would make having conversations very difficult. – SamFord Apr 26 '22 at 13:28
  • ‘a "straight" line on a sphere is what's called a "great circle"’ — eh, it's okay. – Paul D. Waite Apr 26 '22 at 13:38
  • 7
    As a mathematician, let me weigh in. A great circle is a [geodesic](https://en.wikipedia.org/wiki/Geodesic) on a sphere, a notion that _generalizes_ the notion of straight lines in non-curved (Euclidean) spaces. But no mathematician, mapmaker, or anyone else (e.g. a physicist) who has ever spent any time thinking about curved spaces would ever refer to a great circle as a “straight line” except in a way that’s clearly metaphorical, or when addressing a younger audience that you don’t want to intimidate with fancy words (even then you’d emphasize that this is an approximate term only). – Dan Romik Apr 26 '22 at 19:41
  • 5
    … So, while this answer and the other ones are essentially correct, I don’t agree that a great circle is “considered a straight line”. It’s considered the _closest analogue_ (and only meaningful analogue really) to a straight line that one can find on a sphere, and it shares some properties with straight lines, but it’s not considered a straight line in a literal sense. (See also the answer quoting Steven Strogatz, a well-known mathematician, who refers to great circles as the “straightest” paths, which makes it clear he also does not consider them to be “straight lines”.) – Dan Romik Apr 26 '22 at 19:49
  • And ignoring the [Coriolis effect](https://en.wikipedia.org/wiki/Coriolis_force)? – Peter Mortensen Apr 26 '22 at 21:53
  • A look at https://www.youtube.com/watch?v=OH1bZ0F3zVU "Cartographers For Social Equality" is relevant... – DJohnM Apr 27 '22 at 01:26
  • Aviation.SE has some good Q&As you might want to link, including [Explaining a "Great Circle Route" to young Civil Air Patrol cadets](https://aviation.stackexchange.com/q/90567) / [Why don't most planes fly in a straight path?](//aviation.stackexchange.com/q/90717) And also the more advanced point that Earth is *not quite* a sphere, actually an ellipsoid. Modern GPS navigation software has to take that into account, and the shortest path is a geodesic, not necessarily a great circle: [Can a great circle be drawn between any two points on Earth?](//aviation.stackexchange.com/a/92624) – Peter Cordes Apr 27 '22 at 22:56
  • @DanRomik As what type of mathematician? When it comes to projective planes, nobody would talk about anything but lines, even if they don't have parallel lines and the concept of "straight" is simply not relevant in many cases to projective planes. The deeper you get into axiomatics, the more "line" becomes definitely the word to use. – prosfilaes Apr 28 '22 at 04:23
  • 1
    @prosfilaes as the kind of mathematician who knows what he’s talking about. – Dan Romik Apr 28 '22 at 05:04
  • @DanRomik So what are those things in projective planes? What are the components of the Fano plane? – prosfilaes Apr 28 '22 at 15:16
  • 1
    @prosfilaes I don’t know what you’re talking about. If you’re trying to make the point that mathematicians use the word “lines” to mean various things in the context of different mathematical theories, then that is a correct statement, but also has nothing to do with the current discussion. – Dan Romik Apr 28 '22 at 16:02
  • @DanRomik So you're not the kind of mathematician who knows what you're talking about. In elliptical geometry, great circles are lines. Maybe a physicist or an applied mathematician wouldn't use that term, but someone studying models of geometry certainly would. – prosfilaes Apr 28 '22 at 16:18
  • @prosfilaes I am baffled about what kind of rhetorical point you’re trying (and mistakenly thinking you’re succeeding) to score. I said no mathematician would refer to a great circle as a straight line, and I stand by that statement. I have nothing else to add beyond that. – Dan Romik Apr 28 '22 at 16:24
  • @DanRomik Mathematicians in pure geometry and axiomatics would never refer to anything as a "straight line", and would consider Euclidean lines, great circles, and anything else with similar properties lines, as appropriate for the axioms involved. – prosfilaes Apr 28 '22 at 20:56
15

Complementing the existing answers, quoting Professor Strogatz:

For example, when I was little, my dad used to enjoy quizzing me about geography. Which is farther north, he’d ask, Rome or New York City? Most people would guess New York, but surprisingly they’re at almost the same latitude, with Rome being just a bit farther north. On the usual map of the world (the misleading Mercator projection, where Greenland appears gigantic) it looks like you could go straight from New York to Rome by heading due east.

Yet airline pilots never take that route. They always fly northeast out of New York, hugging the coast of Canada. I used to think they were staying close to land for safety’s sake, but that’s not the reason. It’s simply the most direct route, if you take the earth’s curvature into account. The shortest path from New York to Rome goes past Nova Scotia and Newfoundland, then heads out over the Atlantic, and finally veers south of Ireland and across France for arrival in sunny Italy.

This kind of path on the globe is called an arc of a “great circle.” Like straight lines in ordinary space, great circles on a sphere contain the shortest paths between any two points. They’re called “great” because they’re the largest circles you can have on a sphere. Conspicuous examples include the equator and the longitudinal circles that pass through the north and south poles.

Another property that lines and great circles share is that they’re the straightest paths. That might sound strange — all paths on a globe are curved, so what do we mean by “straightest”? Well, some paths are more curved than others. The great circles don’t do any additional curving, above and beyond what they’re forced to do by following the surface of the sphere.

Here’s a way to visualize this. Imagine you’re riding a tiny bicycle on the surface of a globe, and you’re trying to stay on a certain path. If it’s part of a great circle, you won’t ever need to steer. That’s the sense in which great circles are “straight.” In contrast, if you try to ride along a line of latitude near one of the poles, you’ll have to keep turning the handlebars.

Source: Steven Strogatz, Think globally, The New York Times, March 21, 2010.

Bold is mine.

Rodrigo de Azevedo
  • 350
  • 3
  • 16