I've read the odds of dying as around 1 : 250 000 each day, which presumably is based on the global death rate. I use this when people buy lottery tickets to point out they have more chance of dying than winning the money. This forum thread is one example how the odds are worked out, but there are also no doubt plenty of others.
Is this a good way to base it? Is it actually measurable at all? And does this chance increase when you drive a car, fly, cycle etc.?
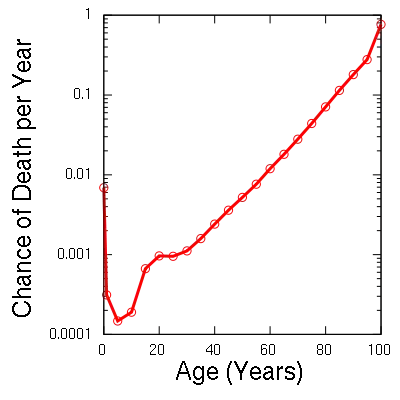 [
[